Введение. Оптимизация — это процесс поиска наилучшего решения при наличии ограничений на ресурсы. В производственных процессах оптимизация помогает минимизировать затраты, ускорить время выполнения операций и использовать ресурсы наиболее эффективно. В условиях ограниченных ресурсов, таких как сырьё, рабочее время и оборудование, важность оптимизации становится особенно актуальной. [5,6]
В современных условиях, когда конкуренция на рынке продуктов питания крайне высокая, оптимизация является ключевым фактором для поддержания прибыльности предприятий. Она позволяет не только снизить производственные издержки, но и улучшить качество продукции, повысить гибкость производства и адаптировать его к изменяющимся рыночным условиям. [4]
Значимость планирования для снижения издержек и повышения эффективности:
Планирование производства необходимо для оптимального распределения ресурсов и минимизации потерь. Для того чтобы сократить затраты и повысить эффективность работы, важно учитывать все доступные ресурсы, их стоимость, а также требования к качеству продукции и скорости её производства. Например, на хлебозаводе оптимизация позволяет точно рассчитать необходимое количество сырья, время работы оборудования и численность персонала, что приводит к значительному снижению издержек. [5,6]
Хорошо спланированное производство позволяет предприятию гибко реагировать на изменения спроса, своевременно удовлетворять потребности рынка и избегать перепроизводства, которое также ведет к лишним расходам. [6]
Примеры оптимизации в пищевой или другой российской промышленности:
В России многие предприятия используют методы оптимизации для повышения конкурентоспособности. Например, на предприятиях молочной промышленности с помощью методов линейного программирования оптимизируют расход сырья и время производства, что помогает повысить доходность. В пищевой промышленности, включая хлебопекарную отрасль, оптимизация с использованием линейного программирования помогает избежать избыточных запасов и излишков продукции, что снижает издержки на хранение и транспортировку. [7,6]
Цель исследования. Целью настоящего исследования является разработка и применение симплекс-метода для оптимизации производственного плана хлебозавода, с целью максимизации прибыли при учёте ограничений на ресурсы, такие как мука, электроэнергия и время работы оборудования. В рамках исследования рассматривается построение математической модели задачи оптимизации, включая целевую функцию и систему ограничений, а также применение симплекс-метода для нахождения оптимальных значений переменных и максимизации прибыли [1, 4, 5, 7].
Материалы и методы исследования. В качестве материала для исследования использовались данные о производственном процессе Омского хлебозавода №1, включая информацию о сырьё (мука, дрожжи), времени работы оборудования и потреблении электроэнергии. Для решения задачи оптимизации использовался симплекс-метод, который является мощным инструментом линейного программирования. Методы исследования включают построение математической модели задачи, формулировку целевой функции и ограничений, а также итерационный процесс поиска оптимального решения с помощью симплекс-метода. Для реализации методов использовалось математическое ПО, обеспечивающее решение задач линейного программирования [6, 7, 9, 10].
Результаты исследования и их обсуждение
Постановка задачи:
Описание производственного процесса:
Омский хлебозавод №1 — одно из крупнейших предприятий в Омской области, специализирующееся на производстве хлебобулочной продукции. Производственные процессы на заводе включают следующие этапы:
- замес теста: этот процесс начинается с загрузки муки, воды и других ингредиентов в миксеры. Здесь также происходит добавление дрожжей и других добавок для улучшения вкуса и текстуры.
- формовка и расстойка: изготовленное тесто делится на порции, формируется в определенные изделия (батоны, буханки, багеты) и оставляется для расстойки.
- выпекание: готовое тесто отправляется в печи, где при температуре 200-250°C происходит выпекание.
- упаковка и транспортировка: после выпекания хлеб фасуется и отправляется в транспортные контейнеры для доставки в магазины и торговые сети.
Основные ограничения (сырьё, мощность оборудования, персонал)
- сырьё: ограниченные запасы муки, дрожжей и других ингредиентов.
- мощность оборудования: ограничение на количество производимой продукции в зависимости от мощности печей, миксеров и других машин.
- персонал: рабочие, занятые на различных этапах, могут работать только в ограниченном количестве часов в день. [6]
Формализация задачи оптимизации:
Цель задачи — максимизация прибыли при ограниченных ресурсах.
Целевая функция: Максимизация прибыли от продажи хлебобулочных изделий, которая зависит от количества произведенной продукции:
,
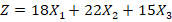где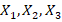 
— количество произведённых единиц пшеничного хлеба, ржаного хлеба и батонов, соответственно, а 18, 22 и 15 — это прибыли от продажи одной единицы продукции. [7]
Теоретическое обоснование симплекс-метода:
Основные принципы и алгоритмы:
Симплекс-метод представляет собой итеративный процесс поиска оптимального решения для задачи линейного программирования. Алгоритм включает несколько ключевых этапов:
- выбор начального базисного решения.
- построение симплекс-таблицы на основе исходных значений.
- итерации, при которых осуществляется переход от текущего решения к следующему, более оптимальному.
- проверка условий завершения: если нет улучшений по целевой функции, то найдено оптимальное решение. [7,9]
Математическая основа линейного программирования:
Линейное программирование решает задачу вида:
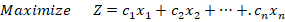
при ограничениях:
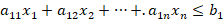
и неотрицательности переменных:
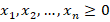[8]
Практическое применение:
Модель оптимизации для выбранного производства:
Для Омского хлебозавода №1 задача оптимизации заключается в максимизации прибыли при учёте ограничений на сырьё, оборудование и рабочее время. Для решения этой задачи применяется метод линейного программирования, что позволяет найти оптимальные значения для количества произведённой продукции с учётом всех ограничений. [9]
Процесс оптимизации включает несколько шагов:
- определение целевой функции: задача максимизации прибыли, которая зависит от количества произведённой продукции. [1]
- формулировка ограничений: учитываются все ограничения, такие как доступное количество сырья, время работы оборудования и энергия. [2, 10]
- решение задачи с помощью симплекс-метода: используется для нахождения оптимального распределения ресурсов и максимизации прибыли. [2, 10]
Этапы решения задачи:
Шаг 1. Формулировка целевой функции
Целевая функция описывает прибыль, которую предприятие получает от продажи хлебобулочных изделий. Пусть:
-
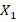— количество произведённого пшеничного хлеба.
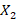— количество произведённого ржаного хлеба.
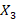— количество произведённых батонов.
Тогда целевая функция будет: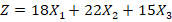
где 18 ,22, 15 — это прибыли от продажи одной единицы продукции, соответственно для пшеничного хлеба, ржаного хлеба и батонов. [5]
Шаг 2. Построение системы ограничений
Для того чтобы эффективно использовать ресурсы, необходимо учесть несколько ограничений:
- ограничение по муке:
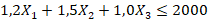(кг).
- ограничение по времени работы оборудования:
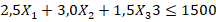(часов).
- ограничение по электроэнергии:
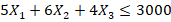(кВт∙ч).
- неотрицательность переменных:
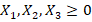[4, 9]
Шаг 3. Решение задачи методом симплекс
Симплекс-метод — это итерационный метод, который используется для решения задачи линейного программирования. Суть метода заключается в том, чтобы улучшать решение, переходя от одной вершины многогранника к другой, пока не будет найдено оптимальное решение.
1. подготовка симплекс-таблицы: на первом этапе формируется начальная симплекс-таблица на основе исходных данных.
2. проверка оптимальности: если решение не является оптимальным, происходит переход к следующей итерации, где будет улучшаться значение целевой функции.
Итерации. В каждой итерации определяется, какой из факторов (переменных) необходимо увеличить или уменьшить для улучшения решения. После нескольких итераций решается задача, и находят оптимальные значения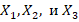 
[2, 8, 10]
Шаг 4. Получение результата
После применения симплекс-метода и нескольких итераций получаем оптимальные значения переменных:
Где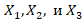 
— это количество произведённых единиц пшеничного хлеба, ржаного хлеба и батонов соответственно.
Оптимальная прибыль, полученная от этих значений:
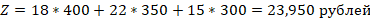
Таблица 1: Пример входных данных для задачи оптимизации
|
Продукт |
Прибыль за единицу (руб.) |
Мука (кг/ед.) |
Время работы (часы/ед.) |
Электроэнергия (кВт*ч/ед.) |
|
Пшеничный хлеб |
18 |
1.2 |
2.5 |
5 |
|
Ржаной хлеб |
22 |
1.5 |
3.0 |
6 |
|
Батон |
15 |
1.0 |
1.5 |
4 |
[3, 7]
Шаг 5. Анализ результатов
После решения задачи и получения оптимальных значений переменных можно провести анализ результатов. Учитывая полученные данные, предприятие сможет:
- использовать ресурсы (муку, время работы оборудования, электроэнергию) наиболее эффективно.
- повысить прибыль за счёт оптимального распределения продукции.
· снизить затраты и повысить конкурентоспособность на рынке. [5, 9]
Шаг 6. Влияние оптимизации на деятельность предприятия
Оптимизация позволяет предприятию значительно сократить операционные затраты. Улучшение планирования производства приводит к следующим выгодам:
- снижение издержек на сырьё и электроэнергию.
- повышение производительности оборудования.
- сокращение времени на производство и доставку продукции.
- увеличение прибыли, что способствует долгосрочной финансовой стабильности и конкурентоспособности предприятия. [6, 10]
Заключение:
Применение линейного программирования и симплекс-метода позволяет значительно повысить эффективность работы предприятия. Пример Омского хлебозавода №1 показал, как с помощью математических методов можно минимизировать затраты и оптимизировать производственные процессы, обеспечивая предприятиям существенные финансовые выгоды.