В настоящее время особенно актуальны проблемы, связанные с проведением уроков в школе. Для оценки уровня математической компетенции и понимания учебного материала, очень важно научить ребенка решать задачи. С самых первых занятий школьники сталкиваются с задачами, и до окончания обучения математические задачи помогают им улучшить свои математические навыки и глубже понять связи между материалом и окружающим миром.
Существуют несколько определений понятия «текстовая задача». Например, Л.М. Фридман считает, что «текстовые задачи представляют собой словесные модели, в которых учащимся надо найти значения (одной или даже нескольких) неизвестной величин. Нахождение таких величин возможно потому, что оно определяется другими неизвестными и известными величинами и их взаимными соотношениями с неизвестной величиной» [3].
Г.В. Бельтюкова и М.А. Бантова под текстовой задачей имеют в виду «жизненную ситуацию, которая связана с числами и решается арифметическими действиями или счетом» [1].
В школьном курсе математики изучают различные методы решения текстовых задач: арифметический, алгебраический, практический, логический, геометрический и др. В основе каждого метода лежат различные виды математических моделей [5].
При любом методе решения, этапы решения текстовой задачи должны включать в себя:
1. Анализ условия задачи;
2. Поиск пути решения задачи и составление плана её решения;
3. Осуществление плана решения задачи;
4. Проверка решения задачи на допустимость.
Решение текстовых алгебраических задач является неотъемлемой частью математического образования в основной школе. Однако, несмотря на то, что все необходимые навыки и знания даются в курсе математики, многие учащиеся испытывают большие трудности при решении таких задач.
Это может быть связано с тем, что задачи этого типа часто содержат большое количество информации, которую нужно правильно интерпретировать и использовать для построения соответствующих алгебраических выражений. Кроме того, такие задачи могут быть построены в несколько этапов, каждый из которых может требовать специальных знаний и умений.
Для успешного решения таких задач учащийся должен иметь глубокое понимание алгебры и уметь применять ее правила для решения сложных задач. Важно, чтобы учитель обращал особое внимание на формирование этих навыков и знаний в процессе обучения.
Основные рекомендации по обучению учащихся решению текстовых алгебраических задач включают в себя:
- Разбор примерных задач на уроке, чтобы ученики могли понять, как применять знания в реальных условиях.
- Привлечение интереса учеников к алгебре через практические задания и игры.
- Использование диаграмм и схем, которые помогут увидеть связь между числами и знаками математических операций.
- Разбиение больших задач на несколько маленьких, что даёт возможность лучше понимать каждую часть задачи.
- Обучение учащихся анализу информации, которая содержится в текстовой формулировке задачи и её перевод на математический язык.
- Упражнения на построение уравнений и систем уравнений на основе содержания текстовой задачи.
Рассмотрим на примере задач на проценты методику решения текстовых задач алгебраическим методом.
Определение процентов похоже на определение дробей и на самом деле проценты тесно связаны с дробями и основаны на них. При работе с задачами на проценты необходимо понимать термины процент, база и процентная ставка. Процент величины – одна сотая часть этой величины, т.е. 
; соответственно, 
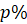от числа a равно 
.
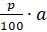Если число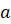 
увеличено на 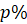, то получится число 
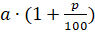; если уменьшено на 
, где 
, то получается число 
.
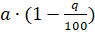Существует несколько методов решения задач на проценты, одним из наиболее простых является использование формул для вычисления процентов. Для решения задач необходимы навыки нахождения процентов от числа и вычисления чисел по известным процентам и частям. Также важно уметь решать задачи, связанные с изменениями базы и процентной ставки, включая увеличение и уменьшение.
Еще один метод решения задач на проценты – это использование пропорций. Для этого нужно записать соотношение, согласно которому две величины связаны между собой, и решить уравнение, которое получается при перемножении крест-накрест.
Примеры задач на проценты:
1. За 2 м ткани одного сорта и 5 м другого сорта заплачено 840 рублей. Если цена первого сорта возрастет на 12,5%, а цена второго сорта на 15%, то на эту покупку придется потратить 950 рублей. Сколько стоит метр ткани каждого сорта?
2. За 1 кг чая и 3 кг сахара заплачено 156 рублей. Если бы цена чая возросла на 25%, а сахара на 10%, то на такую же покупку надо было бы истратить 189 рублей 60 копеек. Что стоит килограмм чая и килограмм сахара?
3. В учебном заведении в двух группах в начале учебного года было 45 учащихся. В середине учебного года перевели из первой группы во вторую двоих учащихся, после чего число учащихся первой группы составило 80% от числа учащихся второй группы. Сколько учащихся было в каждой группе в начале учебного года?
4. В нынешнем году число мальчиков в школе увеличилось на 
числа девочек, бывших в прошлом году в школе, и составило 200 человек; а число девочек увеличилось на 
от числа мальчиков, состоявших в прошлом году в школе, и составило 160 человек. На сколько процентов прибавилось учащихся в школе против прошлого года? Ответ округлите до целого числа.
5. На опытной станции участок пшеницы и участок овса с сорными травами дали всего 1472 кг зерна. По очистке этих участков от сорняков урожайность пшеницы повышается на 80%, а урожайность овса на 24%. После очистки с этих же участков получается 2058 кг зерна. Определить урожайность пшеницы и овса до очистки участков и после.
Продемонстрируем решение задачи №1.
За 2 м ткани одного сорта и 5 м другого сорта заплачено 840 рублей. Если цена первого сорта возрастет на 12,5%, а цена второго сорта на 15%, то на эту покупку придется потратить 950 рублей. Сколько стоит метр ткани каждого сорта?
Решение.Пусть x – стоимость одного метра ткани первого сорта, а y – стоимость одного метра ткани второго сорта. Тогда общая стоимость покупки до повышения стоимости удовлетворяет условию 
После изменения цен за один метр ткани, цена одного метра ткани первого сорта в соответствии с формулой, приведенной выше, стала равной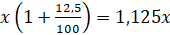 
, аналогично, цена одного метра ткани второго сорта равна сейчас 
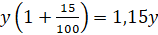. Следовательно, общая стоимость покупки 
.
Получили систему уравнений:
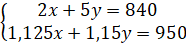
Решим ее методом подстановки, получим
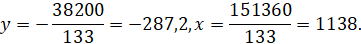
Проверка: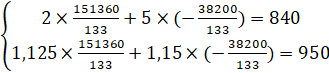 
Ответ: 1138 рублей стоит 1 м ткани первого сорта; -287,2 рубля стоит 1 м ткани второго сорта.
Задача № 2. За 1 кг чая и 3 кг сахара заплачено 156 рублей. Если бы цена чая возросла на 25%, а сахара на 10%, то на такую же покупку надо было бы потратить 189 рублей 60 копеек. Сколько стоят килограмм чая и килограмм сахара?
Решение:
Пусть x - стоимость одного килограмма чая, а y стоимость – одного килограмма сахара. Тогда общая стоимость покупки до повышения цены удовлетворяет условию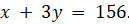 
После изменения цен за один килограмм, цена одного килограмма чая, в соответствии с формулой, приведённой выше, стала равной: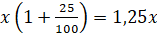 
, аналогично, цена одного килограмма сахара стала равной: 
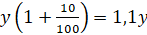. Следовательно, общая стоимость покупки 
.
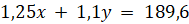Получили систему уравнений:
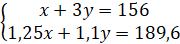
Решим систему методом подстановки, получим
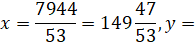
Проверка: 
Ответ: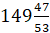 
рублей стоит 1 кг чая; 
рублей стоит 1 кг сахара.
Таким образом, можно сказать, что методические рекомендации по обучению учащихся решению текстовых алгебраических задач должны учитывать специфику задач данного типа и общие особенности обучения учащихся в основной школе. Важно применять разные методы решения, чтобы помочь учащимся эффективнее усвоить данную тему.