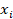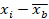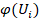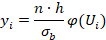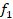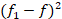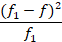Введение. Ассортимент тканей для изготовления сорочечно-платьевых швейных изделий включает хлопчатобумажные, льняные, шерстяные и шелковые материалы. Однако, больше всего используется смешанные шелковые ткани, поэтому при анализе номенклатуры показателей качества тканей сорочечно-платьевого ассортимента следует ориентироваться на ГОСТ 4.51 – 87 СПКП «Ткани и штучные изделия бытового назначения из химических волокон. Номенклатура показателей», ГОСТ 4.6 – 85 СПКП «Ткани шелковые и полушелковые бытового назначения. Номенклатура показателей» [1,2].
Цель исследования. Для более объективной оценки современного ассортимента сорочечно-платьевых тканей целесообразно использовать основные положения математической статистики и теории вероятностей. Для этой цели принимается выборка из генеральной совокупности, которая включает в себя около пятисот артикулов тканей.
Известно, что возможность распространение значений выборки на генеральную совокупность обосновывается теоремой Чебышева, которая верна лишь при соблюдении условий: большого количества измерений, их независимости и случайности выборки. В нашем случае из различных способов организации выборки целесообразно использовать метод таблиц случайных величин [3].
При изучении технологии текстильных материалов с применением математической статистики и теории вероятностей, качественные признаки исследуемого объекта оцениваются с позицией законов распределения. При этом дается полная картина фактического и теоретического распределения. Знание закона распределения дает возможность выявить величину ошибок при определении генеральных характеристик выборки с указанием необходимого объема выборки, обеспечивающего требуемого точность оценки. Кроме того, законы распределения позволяют вывести критерии, дающие возможность судить о влиянии того или иного изменения сырья, технологии или организации производства на качество продукции.
Материал и методы исследования. На законе распределение базируются научно обоснованные расчеты размерного ассортимента при изготовлении одежды, определения оптимального числа стандартных размеров одежды и степени удовлетворенности им населения. Поэтому анализ тканей сорочечно-платьевого ассортимента целесообразно выполнить с позиции нахождения законов распределения.
Для выявления закона распределения тканей сорочечно-платьевого ассортимента необходимо выбрать произвольно из общего количества тканей достаточное число в соответствии с формулой теории вероятностей:
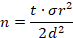
где n – число тканей;
t – числовое значение аргумента t функции Лапласа;
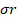– дисперсия выборки;
d – ошибка статистической совокупности.
Так как доверительной вероятности P0= 0,9 соответствует t=1,6 и значение 
приближённо равно 3 в данной совокупности, то по формуле объем выборки тканей смешанного сорочечно-платьевого ассортимента, который должен быть принят для исследований не менее 50 артикулов.
Обработав информацию из технической литературы можно сказать, что показатели свойств швейных изделий чаще всего подчиняются распределению по нормальному закону, гораздо реже – Пуассона и Вейбулла.
Результаты исследования и их обсуждение. Исследуя разрывную нагрузку и несминаемость указанных видов тканей в количестве пятидесяти артикулов и построив статистический ряд их значений по основе и по утку была выдвинута гипотеза о соответствии эмпирического распределения разрывной нагрузки по нормальному закону Гаусса.
Для установления этого факта была составлена таблица 1, по данным которой производились расчеты.
Таблица 1. Распределение разрывной нагрузки шелковых тканей по утку
|
|
|
|
|
|
|
|
15 |
6 |
-27,8 |
-1,78 |
0,0818 |
2,5 |
|
20 |
6 |
-22,8 |
1,46 |
0,1374 |
4,1 |
|
25 |
7 |
-17,8 |
-1,14 |
0,2083 |
6,2 |
|
30 |
7 |
-12,8 |
-0,82 |
0,2850 |
8,6 |
|
35 |
9 |
-7,8 |
-0,5 |
0,3521 |
10,6 |
|
40 |
10 |
-2,8 |
-0,18 |
0,3925 |
11,8 |
|
45 |
12 |
2,2 |
-0,14 |
0,3951 |
11,9 |
|
50 |
10 |
7,2 |
0,46 |
0,3589 |
10,8 |
|
55 |
8 |
12,2 |
0,78 |
0,2943 |
8,8 |
|
60 |
7 |
17,2 |
1,1 |
0,2179 |
6,5 |
|
65 |
6 |
22,2 |
1,42 |
0,1456 |
4,4 |
|
70 |
6 |
27,2 |
1,74 |
0,0878 |
2,6 |
Выявление соответствия эмпирического распределения разрывной нагрузки по утку нормальному закону представлено в таблице 2.
Таблица 2. Выявление соответствия эмпирического распределения разрывной нагрузки по утку по нормальному закону
|
f |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
6 |
3 |
-3 |
9 |
3 |
|
6 |
5 |
-1 |
1 |
0,2 |
|
Продолжение таблицы 2 |
||||
|
1 |
2 |
3 |
4 |
5 |
|
7 |
7 |
0 |
0 |
0 |
|
7 |
9 |
2 |
4 |
0,44 |
|
9 |
11 |
2 |
4 |
0,36 |
|
1 |
2 |
3 |
4 |
5 |
|
10 |
12 |
2 |
4 |
0,33 |
|
12 |
12 |
0 |
0 |
0 |
|
10 |
11 |
1 |
1 |
0,09 |
|
8 |
9 |
1 |
1 |
0,11 |
|
7 |
7 |
0 |
0 |
0 |
|
6 |
5 |
-1 |
1 |
0,2 |
|
6 |
3 |
-3 |
9 |
3 |
В таблице 3 представлен расчет распределения разрывной нагрузки шелковых тканей по основе.
Таблица 3. Распределения разрывной нагрузки шелковых тканей по основе.
|
|
|
|
|
|
|
|
15 |
4 |
-32,2 |
-2,05 |
0,0488 |
1,4 |
|
20 |
4 |
-27,2 |
-1,73 |
0,0893 |
2,6 |
|
25 |
5 |
-22,2 |
-1,41 |
0,1476 |
4,3 |
|
30 |
6 |
-17,2 |
-1,1 |
0,2179 |
6,3 |
|
35 |
6 |
-12,2 |
-0,78 |
0,2943 |
8,5 |
|
40 |
8 |
-7,2 |
-0,46 |
0,3589 |
10,4 |
|
45 |
9 |
-2,2 |
-0,14 |
0,3951 |
11,5 |
|
50 |
10 |
2,8 |
0,18 |
0,3921 |
11,4 |
|
55 |
10 |
7,8 |
0,5 |
0,2850 |
10,2 |
|
60 |
11 |
12,8 |
0,82 |
0,2850 |
8,3 |
|
65 |
11 |
17,8 |
1,13 |
0,2107 |
6,1 |
|
70 |
7 |
22,8 |
1,45 |
0,1394 |
4,1 |
Выявление соответствия эмпирического распределения разрывной нагрузки по основе нормальному закону представлено в таблице 4.
Таблица 4. Выявление соответствия эмпирического распределения разрывной нагрузки по основе нормальному закону.
|
f |
|
|
|
|
|
4 |
2 |
-2 |
4 |
2 |
|
4 |
3 |
-1 |
1 |
0,33 |
|
5 |
5 |
0 |
0 |
0 |
|
6 |
7 |
1 |
1 |
0,14 |
|
6 |
9 |
3 |
9 |
1 |
|
8 |
11 |
3 |
9 |
0,82 |
|
9 |
12 |
3 |
9 |
0,75 |
|
10 |
12 |
2 |
4 |
0,33 |
|
10 |
11 |
1 |
1 |
0,09 |
|
11 |
9 |
-2 |
4 |
0,44 |
|
11 |
7 |
-4 |
16 |
2,29 |
|
7 |
5 |
-2 |
4 |
0,8 |
Распределения несминаемости шелковых тканей по утку представлена в таблице 5.
Таблица 5. Распределения несминаемости шелковых тканей по утку.
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
25 |
1 |
-37,4 |
-3,98 |
0,00014 |
0,007 |
|
30 |
1 |
-32,4 |
-3,45 |
0,00104 |
0,05 |
|
35 |
1 |
-27,4 |
-2,92 |
0,00562 |
0,3 |
|
40 |
3 |
-22,4 |
-2,38 |
0,02349 |
1,2 |
|
45 |
4 |
-17,4 |
-1,85 |
0,07206 |
3,7 |
|
50 |
8 |
-12,4 |
-1,32 |
0,16694 |
8,6 |
|
55 |
14 |
-7,4 |
0,79 |
0,2920 |
15,1 |
|
60 |
19 |
-2,4 |
-0,26 |
0,38568 |
19,9 |
|
65 |
15 |
-2,6 |
0,28 |
0,38361 |
19,7 |
|
70 |
12 |
7,6 |
0,81 |
0,28737 |
14,8 |
|
75 |
8 |
12,6 |
1,34 |
0,16256 |
8,4 |
|
Продолжение таблицы 5 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
80 |
5 |
17,6 |
1,87 |
0,06943 |
3,6 |
|
85 |
2 |
22,6 |
2,4 |
0,02239 |
1,2 |
|
90 |
2 |
27,6 |
2,94 |
0,00530 |
0,3 |
|
95 |
2 |
32,6 |
3,47 |
0,00097 |
0,05 |
Выявление соответствия эмпирического распределения несминаемости по утку нормальному закону представлен в таблице 6.
Таблица 6. Выявление соответствия эмпирического распределения несминаемости по утку нормальному закону.
|
f |
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
3 |
2 |
-1 |
1 |
0,5 |
|
4 |
4 |
0 |
0 |
0 |
|
8 |
9 |
1 |
1 |
0,1 |
|
14 |
16 |
2 |
4 |
0,25 |
|
19 |
20 |
1 |
1 |
005 |
|
15 |
20 |
5 |
25 |
1,25 |
|
12 |
15 |
3 |
9 |
0,6 |
|
8 |
9 |
1 |
1 |
0,1 |
|
5 |
4 |
-1 |
1 |
0,25 |
|
2 |
2 |
0 |
0 |
0 |
|
2 |
1 |
-1 |
1 |
1 |
|
2 |
1 |
-1 |
1 |
1 |
Выводы. В результате проделанной работы изучено распределение основных качественных признаков тканей сорочечно-платьевого ассортимента, в частности такой, как разрывная нагрузка и несминаемость, оцениваемой с позиций законов распределения. При этом получили полную картину фактического и теоретического распределения. Найденные закономерности распределения позволяют сделать следующие выводы.
На рис. 1. представлен график распределения разрывной нагрузки шелковых тканей по утку
Рис. 1. График распределения разрывной нагрузки шелковых тканей по утку
Из приложения 5 учебного пособия теории вероятностей и математической статистики, находим, что при числе степеней свободы 11, т.е. 12-1 и x2 равном 7,73 вероятность соответствия данного эмпирического распределения избранному теоретическому (нормальному) составляет 0,7133, следовательно, для такого распределения модель закона Гаусса приемлема с большой степенью вероятности. [4].
На рис.2 представлен график распределения разрывной нагрузки шелковых тканей по основе
Рис.2. График распределения разрывной нагрузки шелковых тканей по основе
Из приложения 5 учебного пособия теории вероятностей и математической статистики, находим, что при числе степеней свободы 11, т.е. 12-1 и x2 равном 9 вероятность соответствия данного эмпирического распределения избранному теоретическому (нормальному) составляет 0,4433, следовательно, для такого распределения модель закона Гаусса приемлема хотя и с малой степенью вероятности. [4].
На рисунке 3 представлен график распределения несминаемости шелковых тканей по утку
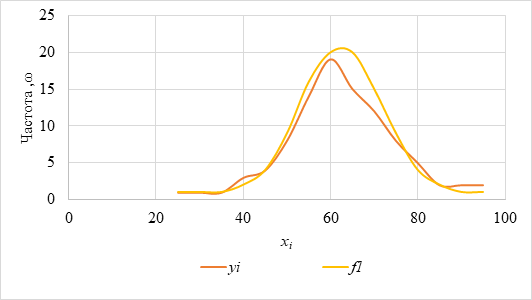
Рис. 3. График распределения несминаемости шелковых тканей по утку
Из приложения 5 учебного пособия теории вероятностей и математической статистики, находим, что при числе степеней свободы 14, т.е. 15-1 и x2 5,54 вероятность соответствия данного эмпирического распределения избранному теоретическому (нормальному) составляет 0,9858, следовательно, для такого распределения модель закона Гаусса приемлема с очень большой степенью вероятности [4].