Матрицы: что это и зачем их используют в науке и технике?
Матрица - это таблица из чисел, которая несет в себе какие-либо данные (строки, например, по одной характеристике, а столбцы - по определенному объекту).
Матрицы используют в линейной алгебре для решения систем уравнений, а также в компьютерной графике при обработке изображений, чтобы преобразовывать картинку и удалять с неё шум. К слову, их широко применяют в статистике для анализа данных и классификации объектов (матрицы ошибок - для оценки точности классификации, а корреляционные матрицы - для изучения степени связи между различными свойствами). А участие матриц в электротехнике: анализ электрических цепей, передачу и обработку сигналов телекоммуникаций, без чего современная жизнь не может существовать.
Примеры “нечетких” понятий в человеческой жизни, нечеткие множества и отношения.
Концепция нечеткости говорит, что иногда встречаются величины, которые могут принадлежать множеству только частично, то есть не точно определены, а значит являются размытыми. Также и понятия "сильный", "широкий" или "дорогой" имеют разное значение в зависимости от условий.
Нечеткие множества используют для интерпретации подобных отношений, а уже в них существую переменные принимающие значения от 0 до 1, в то время как в обычных матрицах существует только 1 и 0, "правда" или "ложь". К примеру множество "высокие люди" может иметь разный диапазон, в зависимости от страны или национальности. Нечеткие множества используют для описания отношений на подобии "очень похож на что-то", "не очень хорошо для чего-то" и т.д., поэтому переменные множества "очень похож на что-то" могут иметь значения от 0 до 1, в зависимости от степени сходства между образцом и условием.
Нечеткость предполагает, что наш мир является неопределенным, а наоборот - размытым и требует введения нечетких множеств и отношений, чтобы его описать.
Нечеткие матрицы: что такое и как отличаются от обычных матриц?
Нечеткие матрицы - это расширение обычных матриц для обработки нечеткой информации, в отличие от обычных матриц, где каждый элемент имеет определенное значение ("истинно" или "ложно"), в нечеткой матрице каждый элемент принимает значение, характеризующее степень его принадлежности к определенному множеству (от 0% до 100%).
Стандартные операции, при работе с обычными матрицами не всегда могут подходить для нечетких. То же умножение (конъюнкция или же пересечение, если речь идет о множествах) может привести к некорректному результату и поэтому существуют специальные методы.
Допустим, у нас есть две нечеткие матрицы A и B размером 3 на 3, заданные следующим образом:
Выполним обычное умножение нечетких матриц A и B:


В полученной матрице C значения получились слишком маленькими по сравнению с исходными матрицами. Это связано с тем, что при умножении A и B происходит сильное размытие исходных данных. Способом исправления является более точный метода умножения. Он основан на том, что в результате будет выбран минимальный из двух элементов матриц A и B. Другими словами, если a_ij и b_ij (i и j - индексы позиции элемента в матрице) являются нечеткими элементами, то результат будет равен min(a_ij, b_ij).
Умножим снова наши матрицы A и B. Для каждого элемента c_ij матрицы C необходимо найти минимальное значение, которое может быть получено путем взятия минимума из элементов a_ij и b_ij:
c_11 = min(0.2, 0.1) = 0.1
c_12 = min(0.4, 0.6) = 0.4
c_13 = min(0.7, 0.8) = 0.7
c_21 = min(0.5, 0.2) = 0.2
c_22 = min(0.9, 0.3) = 0.3
c_23 = min(0.1, 0.5) = 0.1
c_31 = min(0.8, 0.7) = 0.7
c_32 = min(0.3, 0.4) = 0.3
c_33 = min(0.6, 0.9) = 0.6

В результате получилась нечеткая матрица, которая является результатом умножения матриц A и B.
Неопределенность и нечеткость в данных: классификация объектов, кластеризация, распознавание образов, моделирование нечетких правил, прогнозирование временных рядов.
При классификации объектов не всегда можно определить, к какому классу они относятся, тогда нечеткие матрицы помогают представить неопределенность в виде чисел, отражающих степень принадлежности объекта к каждому из классов, а вот нечеткие матрицы фигурируют в кластеризации данных, то есть разбиения множества объектов на группы по схожести.
Ещё такие матрицы используют для прогнозирования временных рядов - оценка взаимосвязи между различными переменными и предсказание возможных тенденций.
Различные методы и подходы работы с нечеткими матрицами.
Теория нечетких множеств: элементы нечеткой матрицы представляют нечеткие множества, которые описывают степень принадлежности элементов к определенным классам. Один из самых простых и интуитивно понятных методов, но неэффективен при работе с большими объемами данных.
Алгебра нечетких чисел: арифметические операции (сложение, умножение и деление, усиление и ослабление) выполняют над нечеткими матрицами в задачах прогнозирования и моделирования, но этот метод требует более сложных вычислений и поэтому его трудно использовать в объемных проектах.
Нечеткая логика: логические операции (конъюнкция, дизъюнкция, отрицание и др.) над нечеткими матрицами и решение задач классификации и распознавания образов.
Кроме перечисленных, существует множество других подходов к работе с нечеткими матрицами: алгоритмы генетического программирования и машинного обучения.
Польза от нечетких матриц: где они могут быть неэффективными?
Нечеткие матрицы в различных отраслях:
1. Нечеткая логика и системы управления: нечеткие матрицы используют при решении задач управления и принятия решений.
2. Медицина: анализ медицинских данных и принятие решений в диагностике и лечении заболеваний.
3. Компьютерное зрение: обработка изображений и распознавание образов.
4. Информационные технологии: анализ и обработка больших библиотек данных в машинном обучении и ИИ.
5. Инженерия: оптимизация процессов проектирования и управления производством.
6. Финансы: анализ рисков и принятие инвестиционных решений.
7. Социология и психология: анализа социальных и психологических данных, например, для изучения предпочтений и оценок людей, другими словами статистика.
Преимущества:
1. Универсальность. Использование во многих областях.
2. Устойчивость к шуму. Нечеткие матрицы могут обрабатывать данные с шумом и помехами.
3. Гибкость. Нечеткие матрицы можно легко изменить и настроить для решения различных задач.
Недостатки:
1. Сложность интерпретации. Нечеткие матрицы могут быть сложными для понимания и интерпретации.
2. Необходимость большого количества данных. Для создания нечеткой матрицы необходимо иметь большой объем библиотек для обучения.
3. Вычислительная сложность. Обработка нечетких матриц может требовать значительных вычислительных ресурсов.
Нечеткие матрицы в игровых механиках.
В механике игр и управлении неигровыми персонажами нечеткие матрицы используют для принятия решений. Рассмотрим задачу управления боевым NPC в игре:
Для того чтобы он мог принимать решения, надо иметь информацию о текущем состоянии игрового мира. NPC может видеть только часть поля или получать данные о положении противников с погрешностью. В таком случае нечеткие матрицы используют для представления информации о состоянии игрового мира и на основе этой информации принимается решение, влияющее на поведение NPC (расстояние до противника, личный уровень здоровья и т.д.).
Вот так и определяется поведение NPC: если расстояние до противника маленькое и личный уровень здоровья высок, то NPC выбирает действие атаки, а если расстояние большое и личный уровень здоровья низкий, то NPC решает остаться незамеченным.
Мы также можем самостоятельно составить собственную матрицу в 2, 3 и более измерений. Предположим, есть персонаж, которому могут нанести различный вид урона: низкий, средний и критический; и так же характеристики, которые могут добавить определенный коэффициент к нанесенному урону: голод и жажда. Создадим нашу матрицу:
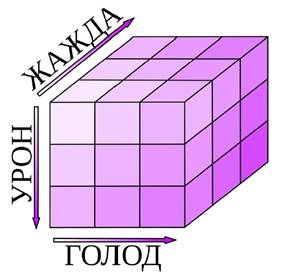
Как мы видим, чем больше жажда и голод, тем больше наносится урон.
Нечеткие матрицы эффективный инструмент для работы с нечеткостью в данных. Их используют в моделировании нечетких правил, классификации объектов, кластеризации данных, распознавания образов, прогнозирования временных рядов и д.р.
Использование нечетких матриц в системе теории принятия решений - хорошее преимущество, ведь именно с этими способностями открыто много новых функций, как например, моделирование человеческого мышления у ии, но это все еще будет требовать большую вычислительную мощность.

