Рак – это общее обозначение большой группы болезней, которые могут поражать любую часть тела. Используются также такие термины, как злокачественные опухоли и новообразования. Характерным признаком рака является быстрое образование аномальных клеток, прорастающих за пределы своих обычных границ и способных проникать в близлежащие части тела и распространяться в другие органы. Этот процесс называется метастазом. Метастазы являются основной причиной смерти от рака [1].
Проникновение математических методов в самые разнообразные, подчас неожиданные сферы человеческой деятельности означает возможность пользоваться новыми, как правило, весьма плодотворными средствами исследования.
В последние годы в медицину активно внедряются методы математического моделирования.
В практике математического моделирования исходным пунктом часто является некоторая эмпирическая ситуация, выдвигающая перед исследователем задачу, на которую требуется найти ответ. Часто параллельно с этой стадией постановки задачи идёт процесс выявления основных или существенных факторов процесса. В частности для физических явлений этот процесс схематизации или идеализации играет решающую роль, поскольку в реальном явлении участвует множество явлений и оно чрезвычайно сложно [2].
После того как существенные факторы выявлены, следующий шаг состоит в переводе этих факторов на язык математических понятий и величин и постулировании соотношений между этими величинами. После построения модели её следует подвергнуть проверке. Адекватность модели до некоторой степени проверяется обычно в ходе постановки задачи. Уравнения или другие математические соотношения, сформулированные в модели, постоянно сопоставляются с исходной ситуацией.
Раковая клетка, изначально лишенная доступа к крови, а значит и доступа кислорода, находится в невыгодных условиях - чтобы выжить раковая клетка должна потреблять в 19 раз больше глюкозы, чем обычная клетка.
В условиях здорового организма это практически невозможно, поэтому мутированная клетка очень быстро погибает от недостатка питания. Это и есть действие естественного отбора на клеточном уровне.
Здоровая клетка получает из крови холестерин, глюкозу и кислород. Именно кислород позволяет здоровой клетке эффективно усваивать глюкозу.
Раковая клетка не имеет доступа к крови, получает от соседних здоровых клеток холестерин и глюкозу. Кислорода она не получает, а преобразует глюкозу в АТФ путем брожения.
Следовательно, для того, чтобы смогла выжить раковая клетка, окружающие ее здоровые клетки должны быть поставлены в непредусмотренные эволюцией неблагоприятные условия. Только если здоровая клетка в 19 раз меньше получит кислорода [3], чем ей нужно, только в этом случае раковая клетка сможет существовать наравне со здоровой и порождать себе подобные раковые клетки.
Если такая ситуация случится, то начинается медленный, очень медленный рост опухоли. Этот рост может идти от 3 до 20 лет. В результате безкислородного гликолиза вокруг опухоли начинает образовываться молочная кислота, которая, так как опухоль не имеет никаких кровеносных сосудов, никуда не выводится, а просто накапливается около опухоли. Это мешает нормальному функционированию окружающих опухоль клеток, сдавливает эти клетки, ткани, сосуды, нервы.
Молочная кислота - ценный для организма продукт, даже ценнее глюкозы, и организм попадает в ловушку - он пытается использовать эти запасы молочной кислоты и капилляры кровеносной системы начинают прорастать в опухоль, чтобы использовать эту молочную кислоту.
С прорастанием капилляров кровеносной системы в опухоль ради извлечения и удаления запасов молочной кислоты, начинается самый опасный этап развития опухоли. Клетки опухоли получают доступ к кислороду, и вместе с ним начинают извлекать из того же количества глюкозы, что у них было в 19 раз больше энергии. Опухоль начинает развиваться неудержимо, образуются метастазы. Обычно этот процесс начинается в тот момент, когда опухоль состоит примерно из 600тыс. - 1 млн. клеток.
Поэтому о профилактике опухолей имеет смысл говорить только до начала этого процесса прорастания капилляров в опухоль, когда развитие опухоли еще зависит от состояния окружающих ее тканей и от нормального их питания. В этот период клетки опухоли получают питание (глюкозу и холестерин) от соседних здоровых клеток. Когда же опухоль прорастает капиллярами, клетки опухоли начинают получать питание непосредственно из крови, тут уже речь может идти не о профилактике, а только о лечении.
Вся профилактика опухолей сводиться к тому, чтобы обеспечить здоровые клетки организма полноценным питанием.
Это необходимое и достаточное условие профилактики любых форма рака. Только в этом случае мутированные клетки не смогут выжить.
Больше того – так как в каждую секунду в нашем организме существует 10 млн. мутированных (раковых) клеток, возникающих во всех тканях организма, эту профилактику следует проводить ежедневно и ежечасно, чтобы не допустить размножения этих "испортившихся" клеток.
Обсудим питание, которое должна получать здоровая клетка, а именно глюкозу, холестерин, кислород.
Нормальный уровень глюкозы в крови 3,33 - 5,55 ммоль/л создает наиболее благоприятные условия для клеток организма. Но чем выше обеспечение здоровых клеток глюкозой, тем это более выгодно опухолевым клеткам, т.к. чрезмерно обеспеченные здоровые клетки, окружающие опухоль, в этом случае снабжают опухолевые клетки более обильно.
Следовательно, для профилактики рака надо поддерживать в крови уровень глюкозы на уровне 3,5 - 4,0 ммоль/л, т.е. несколько пониженный, но в пределах нормы. В этом случае здоровые клетки перестанут обеспечивать клетки опухоли глюкозой, и произойдет обратное развитие опухоли.
Таким образом, становится понятно, почему ожирение и избыточный вес являются факторами, способствующими возникновению рака. При ожирении, как правило, и несколько повышено содержание сахара в крови, и значительно усилен обмен глюкозы. "Сытые" здоровые клетки становятся более щедрыми и полноценно снабжают своих опухолевых соседей достаточным количеством глюкозы [4].
Проведено порядка ста исследований по профилактике онкологических заболеваний с помощью ликопина или ликопин-содержащих продуктов. Данные противоречивые, что связано с косвенным характером экспериментов. Установлено, что риск развития некоторых видов рака обратно пропорционален содержанию в крови (или суточному потреблению) ликопина. Такие выводы можно сделать в отношении рака простаты, желудка и легких.
Показано, что риск развития атеросклероза и связанных с ним ишемических заболеваний обратно пропорционален содержанию в крови (или суточному потреблению) ликопина.
Предлагаемая математическая модель роста опухолевых клеток содержит три типа клеток:
1 . Активно делящиеся и подвижные клетки опухоли (обозначим их плотность n).
2.Неделящиеся и не обладающие собственной подвижностью клетки опухоли (обозначим их плотность m), этот тип клеток отражает как опухолевые клетки в состоянии покоя, так и мёртвую клеточную массу.
3.Клетки здоровой ткани, не обладающие собственной подвижностью.
Клетки первой группы могут необратимо переходить во вторую. Это отражает прекращение пролиферации при неблагоприятных условиях. Клетки всех типов переносятся конвективными потоками, возникающими из-за избыточной клеточной массы в области активного роста. Подвижные клетки опухоли также способны распространяться за счет случайных блужданий и направленно - за счет хемотаксиса. Клетки опухоли могут подавлять клетки здоровой ткани.
Обозначим S концентрацию ключевого питательного вещества (играющего роль лимитирующего фактора), в описываемой постановке задачи таким веществом считается кислород. Тогда рост опухоли в среде может быть описан следующей системой уравнений:
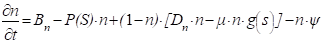 , (1)
, (1)
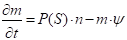 , (2)
, (2)
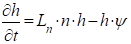 , (3)
, (3)
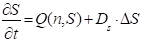 , (4)
, (4)
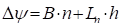 . (5)
. (5)
Здесь B > 0 – мальтузианская скорость роста популяции опухолевых клеток, L – коэффициент интенсивности парного взаимодействия клеток опухоли и клеток здоровой ткани, 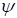 - потенциал скорости,
- потенциал скорости, 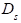 - коэффициент диффузии питательного вещества S.
- коэффициент диффузии питательного вещества S.
Интенсивность превращения подвижных опухолевых клеток в неподвижные (процесс считается необратимым) описывается функцией 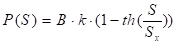 , где k, Sх – параметры модели. Такой вид функций позволяет учитывать прекращение пролиферации при недостатке питательных веществ [5].
, где k, Sх – параметры модели. Такой вид функций позволяет учитывать прекращение пролиферации при недостатке питательных веществ [5].
Потребление питательного вещества описывается функцией
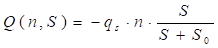 , где qs, S0 – параметры модели, Q(n,S) < 0.
, где qs, S0 – параметры модели, Q(n,S) < 0.
Предполагается, что питательные вещества потребляются в основном делящимися клетками.
Собственная подвижность делящихся клеток учтена добавлением в (2.3а) диффузионных членов: Dn – коэффициент диффузии, 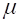 - коэффициент хемотаксиса по отношению к ключевому питательному веществу, g(s) – функция полезности питательного вещества, определенная как
- коэффициент хемотаксиса по отношению к ключевому питательному веществу, g(s) – функция полезности питательного вещества, определенная как 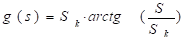 , где
, где 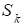 - параметр модели.
- параметр модели.
Такая модель учитывает размножение опухолевых клеток за счет деления, прекращения деления состарившихся клеток, взаимное подавление делящихся опухолевых клеток и клеток здоровой ткани, потребление питательного вещества опухолевыми клетками и клетками здоровой ткани, а также конвективное «течение» тканей и собственную подвижность опухолевых клеток [6].

