При исследовании различных динамических систем часто используются имитационные модели. Согласно одному из определений, имитационная модель это определенный алгоритм, описывающий функционирование системы во времени, реализация которого осуществляется с помощью соответствующей машинной программы.
При невозможности описать весь спектр воздействующих на систему факторов в модель вводится элемент случайности. Таким образом, для работы моделирующей программы необходима генерация случайных чисел.
Компьютерная программа, работающая по определенному алгоритму, может генерировать только псевдослучайные числа. Результаты работы различных алгоритмов проверяются статистическими тестами. Для генерации случайных чисел в программу подставляются случайным образом начальные условия. Для моделирования могут быть необходимы случайные величины с самыми разными характеристиками, но обычно, сначала генерируется базовая последовательность случайных чисел. Совокупность независимых, равномерно распределенных на отрезке [0,1] случайных величин Ri , (i=0,1…) называется последовательностью базовых случайных чисел. Гистограмма, показывающее равномерное распределение величин представлена на рисунке 1.
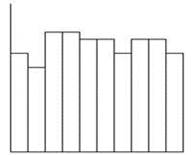
Рисунок 1 – Гистограмма равномерного распределения величин
Алгоритм Лемера
Американский исследователь Д. Лемер предложил метод генерации базовой последовательности, представимый в виде формулы или реккурентного соотношения.
Алгоритмы Лемера получения псевдослучайных чисел Ri+1 имеют достаточно простой вид: Ri+1 = F (Ri), i=0,1, …
Начальное число R0 задано, а все последующие числа R1, R2, … вычисляются по одной и той же формуле. Заметим, что метод серединных квадратов, рассмотренный выше, также имеет аналогичный вид, но вместо аналитического задания функции y=F(x) была указана совокупность операций, которые надо проделать над аргументом x, чтобы получить значение y.
Рассмотрим, какие требования необходимо предъявлять к функции F(x), чтобы последовательность удовлетворяла требованиям, предъявляемым к базовой последовательности, т.е. числам, равномерно распределенным на отрезке [0, 1]
Рассмотрим пример, позволяющий понять, в чем состоит одна из основных трудностей при выборе F(x). Во-первых, аргумент и значение функции не должны выходить за пределы отрезка [0, 1]. Но это не все. Произвольная функция, например, график которой показан на рис.2 а) не подходит для генерации случайных чисел, поскольку все точки будут сконцентрированы на кривой, а настоящие случайные точки должны равномерно заполнять весь единичный квадрат.
Таким свойством y = {g·x}, где g – очень большое число. Символ×обладает, например, функция фигурных скобок {*} означает дробную часть числа *.
На рис. 2,б-в) построен график функции y = {g·x}, при не очень больших числах они равны в случае б) g=5, и в) g=20.
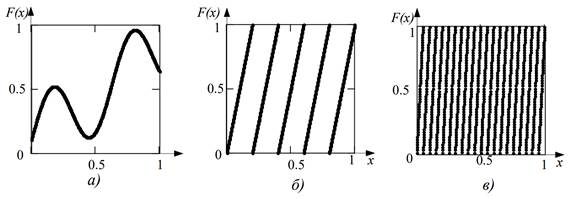
Рисунок 2 – функции F(x), использующиеся в алгоритме Лемера
Блок-схема данного алгоритма представлена на рисунке 3.
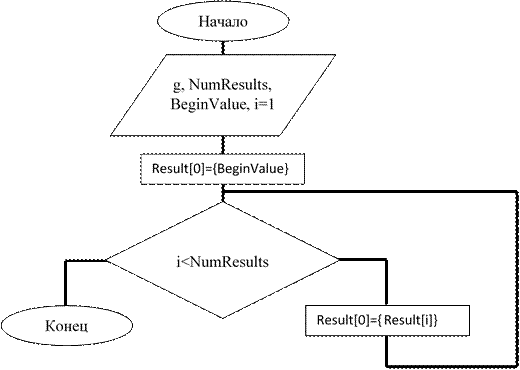
Рисунок 3 – Блок-схема реализации алгоритма Лемера
Программная реализация данного метода на языке программирования java script представлена на рисунке 4.
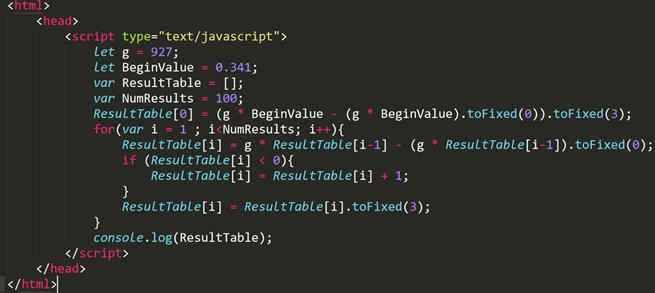
Рисунок 4 – Реализация метода на языке программирования java script
Конгруэнтный мультипликативный метод Лемера
В настоящее время, почти все стандартные библиотечные программы вычисления случайных базовых чисел основаны на конгруэтном методе, или методе сравнений.
Основная формула мультипликативного конгруэнтного метода имеет вид:
Xi+1 = aXi(mod m),
где а и m — неотрицательные целые числа.
Согласно этому выражению, мы должны взять последнее случайное число Ri , умножить его на постоянный коэффициент а и взять модуль полученного числа по m (разделить аXi на m и остаток считать как Xi+1).
Выбираются а, X0 и m так, чтобы обеспечить максимальную длину (или, как говорят, период) неповторяющейся последовательности Xi и минимальную корреляцию между генерируемыми числами. В результате получается последовательность псевдослучайных чисел равномерно распределенных на интервале от 0 до m. Для того чтобы получить базовую последовательность, нужно разделить все числа последовательности Xi на m. Ri =Xi/m.
Блок-схема данного алгоритма представлена на рисунке 5.
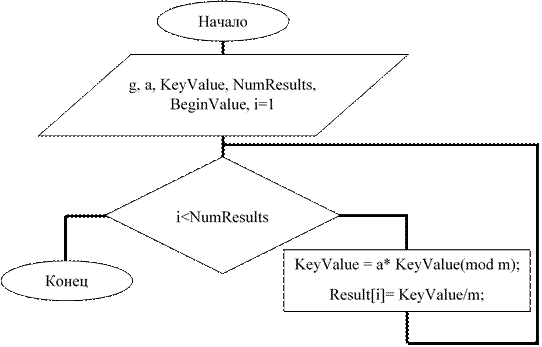
Рисунок 5 – Блок-схема конгруэнтного мультипликативного метода Лемера
Программная реализация данного метода на языке программирования java script представлена на рисунке 6.
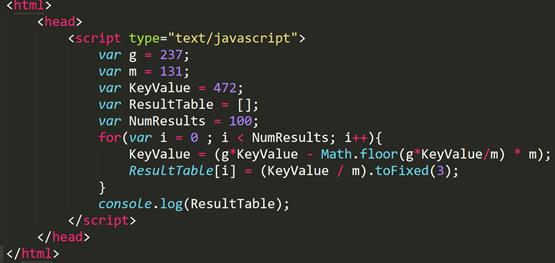
Рисунок 6 – Реализация конгруэнтного мультипликативного метода Лемера на языке программирования java script

