При проектировании САУ довольно часто решается задача определения оптимальных параметров системы.Эти задачи можно решать на основе единственного подхода, основанного на поисковой процедуре, организованной по определенному алгоритму, входящему в состав методов нелинейного программирования.
В зависимости о числа поисковых переменных различают одномерный и многомерный поиски. В качестве самостоятельной процедуры одномерный поиск применяют сравнительно редко, однако его часто используют как важный элемент многомерного поиска.
Из существующих методов одномерного поиска наиболее распространенные два метода:
1. метод дихотомии;
2. метод золотого сечения.
По указанным методам будут приведен алгоритмреализации и блок-схема, наглядно показывающаяпорядок и логику работы метода дихотомии. Также представлен пример решения уравнения при помощи метода дихотомии.
Метод дихотомии систем основан на поиске находящегося в интервале неопределённости, экстремума функции, одной переменной путем деления пополам интервала, на котором находится экстремум[1].
Алгоритм поиска экстремума методом дихотомии состоит из двух групп блоков:
1. Поиск интервала неопределенности;
2. Поиск экстремума на интервале неопределенности с установленной точностью.
На первой этапе вычисляется x0=(a+b)/2.
Далее определяется значение функции в этой точке:
1. если f(x0)< 0, то [a,x0];
2. если наоборот, то [x0,b].
То есть происходит сужение интервала. Таким образом, в результате формируется последовательность xi, где i - номер иттерации.
Вычисления прекращаются, когда разность b-a меньше требуемой погрешности.
В качестве примера использования метода половинного деления найдем корень на интервале [0;1] уравнения x3-3*x+1=0 с точностью в 10-3.
Таблица 1-Поиск корней уравнения
|
n |
a |
b |
xn |
f(xn) |
|
|
0 |
1,0000 |
1,9000 |
1,4500 |
-0,3014 |
Решение не получено |
|
1 |
1,4500 |
1,9000 |
1,6750 |
0,6744 |
Решение не получено |
|
2 |
1,4500 |
1,6750 |
1,5625 |
0,1272 |
Решение не получено |
|
3 |
1,4500 |
1,5625 |
1,5063 |
-0,1014 |
Решение не получено |
|
4 |
1,5063 |
1,5625 |
1,5344 |
0,0093 |
Решение не получено |
|
5 |
1,5063 |
1,5344 |
1,5203 |
-0,0470 |
Решение не получено |
|
6 |
1,5203 |
1,5344 |
1,5273 |
-0,0191 |
Решение не получено |
|
7 |
1,5273 |
1,5344 |
1,5309 |
-0,0050 |
Решение не получено |
|
8 |
1,5309 |
1,5344 |
1,5326 |
0,0021 |
Решение не получено |
|
9 |
1,5309 |
1,5326 |
1,5317 |
-0,0014 |
Решение не получено |
|
10 |
1,5317 |
1,5326 |
1,5322 |
0,0004 |
Решение получено |
Как видно из таблицы корнем является 1,5322. Количество итераций равно 10.
Интервал неопределённости выбирается таким образом, чтобы гарантированно включать в себя точку экстремума [5].
На рисунке 2 представлена блок-схема алгоритма поиска экстремума на интервале неопределенности с установленной точностью по методу дихотомии[3,4].
a,b – точки, между которых заключен интервал неточности, содержащий экстремум функции.
e – установленная точность нахождения экстремума, при достижении которой поиск прекращается.
f() – функция, для которой находится значение экстремума.
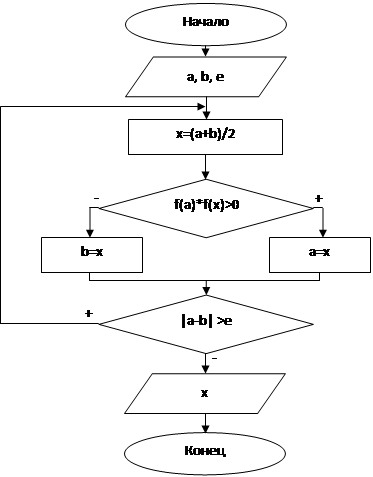
Рисунок 2 - Блок-схема алгоритма поиска экстремума по методу дихотомии
Исходя из анализа, можно сделать вывод, что метод половинного деления, не смотря на свою простоту, требует отделения корня, и для достижения высокой точности приходится вычислять функцию много раз. Однако, достижение заданной точности в этом методе гарантировано, и такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции.
В методе золотого сечения каждая из точек x1 и x2 делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т.е. равно так называемому "золотому отношению"[6].
Это соответствует геометрическому представлению на рисунке 9.
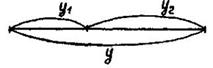
Рисунок 9 - Геометрическое представление золотого сечения
Таким образом, длина интервала неопределенности на каждом шаге сжимается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем – одно[7].
Алгоритм метода золотого сечения для минимизации функции f(x) складывается из следующих этапов:
1. Вычисляется значение функции f(x1), где x1=a+0,382(b-a).
2. Вычисляется значение функции f(x2), где x2=b+0,382(b-a).
3. Определяется новый интервал (a,x2) или (x1,b), в котором локализован минимум.
4. Внутри полученного интервала находится новая точка, отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f(x). Затем вычисления повторяются, пока величина интервала неопределенности станет меньше или равна e.
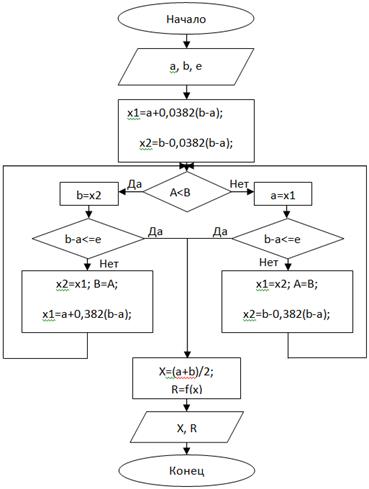
Рисунок 10 - Блок-схема алгоритма поиска экстремума по методу золотого сечения.
На рисунке 10 представлена блок-схема алгоритма поиска экстремума на интервале неопределенности с установленной точностью по методу золотого сечения.
При сравнении описанных в данной статье методов можно отметить, что каждый из рассмотренных методов имеет свои достоинства и недостатки. Метод дихотомии наиболее прост и понятен для реализации, при этом этот метод требует наибольшее количество итераций для получения результата. Метод золотого сечения в свою очередь является наиболее быстродействующим методом и требует наименьшее число итераций для поиска экстремума функции, но в свою очередь требует больших операционных затрат на каждой итерации.
Исходя из выше описанного, можно сделать вывод, что каждый метод имеет свои преимущества и недостатки и может найти применение в различных ситуациях.

