Введение
Студенты младших курсов вуза проявляют разную успешность в учебном процессе. Достаточно продолжительный курс математики позволяет заметить, что кто-то из них практически сразу включается в учебную рутину, посильно выполняя задания и сохраняя постоянный уровень усилий. Другие демонстрируют бодрый старт и слабое продолжение, связанное с появлением новых внеучебных интересов [1]. Третьи, напротив, адаптируясь в новых условиях, чувствуют себя лучше [2, 3, 4]. Четвертые учатся неравномерно. Большое количество разнонаправленных факторов интегрально отражается на показателях академической успеваемости, которые образуют массивы данных и могут быть подвергнуты численной обработке. Мы изучили возможности прогнозирования изменений показателей успеваемости во времени и оценки надежности такого прогноза с помощью математического моделирования [5].
Цель исследования
Разработка приемов математического моделирования показателей успеваемости студентов в динамике. Выявление закономерностей эволюции академической успеваемости путем сравнения фактических данных с модельной ситуацией.
Материал и методы исследования
Частный математический аппарат исследования – марковские цепи с дискретным временем перехода (МЦ), традиционно входящие в состав раздела современной математики, известного как «Исследование операций» [6]. При этом мы интерпретировали оценки студентов за текущие контрольно-отчетные мероприятия (КОМ – контрольные и расчетно-графические работы), как состояния марковской цепи, а их сохранение или изменение от одной работы к другой – как переходы. В качестве эмпирической основы исследования был взят массив оценок, полученных в потоке студентов, обучающихся по специальности «Эксплуатация железных дорог» 2018 год набора (около 150 студентов) за первый курс обучения, т.е. 8 КОМ, около 1,2 тыс. частных оценок и 1 тыс. переходов между ними. Для расчетов использован MS EXCEL 2007.
Для моделирования использовалась МЦ с тремя состояниями: 1 – оценка за КОМ ещё не получена или работа зачтена с минимальным баллом; 2 – «хорошо», 3 – «отлично».
Особенность регулярных марковских цепей, как системных объектов, – наличие «стационарного» распределение вероятностей состояний. Для нахождения данного распределения мы определяли матрицу условных вероятностей перехода, затем составляли и решали систему линейных алгебраических уравнений, вытекающих из данной матрицы, для поиска стационарных значений. Полученный результат может интерпретироваться как вероятностный прогноз «предельного» распределения.
Далее мы моделировали пошаговую эволюцию марковской цепи путем многократного умножения вектора распределения вероятностей состояний на матрицу переходов, – для уточнения полученного результата. Наконец, для оценки надежности вероятностного прогноза было предпринято специальное исследование, в котором стационарные распределения были получены несколько раз и сопоставлены друг с другом.
Анализ общей совокупности данных
В табл. 1 представлен результат поиска элементов матрицы условных вероятностей перехода – по всей совокупности данных, полученных за первый курс, это восемь КОМ за два семестра. Далее представлена матрица условных вероятностей переходов и система линейных алгебраических уравнений, решаемая для нахождения стационарного распределения. В итоге, получено стационарное распределение вероятностей состояний марковской цепи – примерно 2/3 случаев в первом состоянии, по 1/6 – во втором и третьем.
Таблица 1
|
Исходное состояние |
Кол-во реализаций исходного состояния |
Переход |
Кол-во реализаций перехода |
Усл. вероятность перехода |
|
1 |
604 |
11 |
552 |
0,914 |
|
12 |
38 |
0,063 |
||
|
13 |
14 |
0,023 |
||
|
2 |
209 |
21 |
52 |
0,249 |
|
22 |
117 |
0,560 |
||
|
23 |
40 |
0,191 |
||
|
3 |
230 |
31 |
15 |
0,065 |
|
32 |
48 |
0,209 |
||
|
33 |
167 |
0,726 |
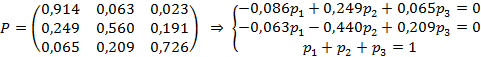
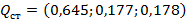
Пошаговое моделирование эволюции МЦ и сравнение с эмпирическими данными
Для более глубокого понимания протекающего процесса найденное стационарное (предельное) распределение вероятностей требуется сравнить с эмпирическими данными. Для этого проведем пошаговое моделирование эволюции МЦ построим графики, характеризующие динамику вероятности каждого из состояний, путем многократного умножения исходного распределения вероятностей состояний (оно было взято по результатам первой КОМ) на матрицу вероятностей переходов Р. Синяя линия на каждом графике обозначает реальную динамику вероятности состояния (поэтапно, от одной КОМ к другой), оранжевая линия показывает смоделированную динамику, серая показывает стационарное состояние.
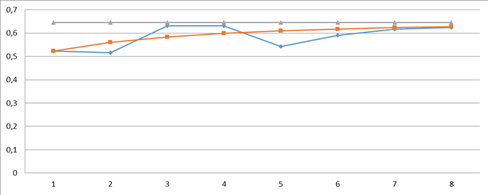
Рис. 1. Динамика p1: фактическая и модельная, стационарное значение
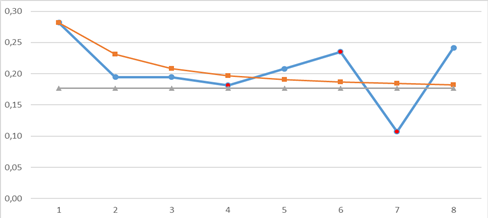
Рис. 2. Динамика p2: фактическая и модельная, стационарное значение
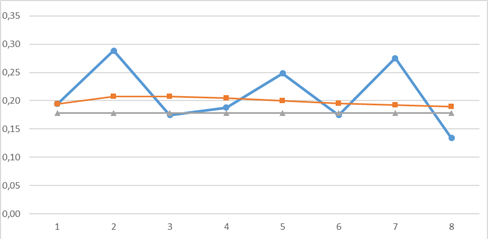
Рис. 3. Динамика p3: фактическая и модельная, стационарное значение
Исходя из графиков, можно сделать промежуточные выводы:
– За 8 шагов МЦ НЕ ДОСТИГАЕТ стационарного (предельного) распределения;
– Показатели успеваемости демонстрируют сложную разнонаправленную эмпирическую динамику, требующую дополнительного объяснения;
– В наибольшей степени результаты моделирования совпадают с эмпирическими данными для р1 (нижний уровень успеваемости).
Оценка надежности вероятностного прогноза
Рассмотрим переходы между смежными КОМ по отдельности. Каждая такая пара КОМ характеризуется парой оценок для всех студентов (около 150 человек, семь пар - переходов) и может быть обработана аналогично общему массиву данных. Если частные результаты таких действий будут близки между собой и с общим результатом, это будет свидетельством надежности (устойчивости) прогноза. Заметим, что непосредственно сравнивать между собой матрицы условных вероятностей переходов, продемонстрированных студентами на каждом этапе в отдельности, затруднительно из-за отсутствия наглядного критерия их взаимной «удаленности». Однако, каждой такой матрице соответствует некоторое стационарное распределение и совокупность прогнозов, полученных, например, для вероятности первого состояния, исследовать уже гораздо проще.
Сравнение стационарных вероятностей, полученных по поэтапным значениям условных вероятностей переходов показано на рис. 4 (горизонтальные штрихи показывают частные прогнозируемые стационарные значения, синий крест – стационарное значение, полученное по всей совокупности данных, а красный крест – среднее арифметическое от частных значений). Как видно по графику, опираясь на результаты отдельных КОМ и переходы, продемонстрированные в них, можно получить прогнозы распределения вероятностей с большим разбросом. Мы объясняем это тем, что трудности изучения разных разделов курса и выполнение связанных с ними работ, а также разнообразные неучтенные внешние факторы, влияющие на учебную жизнь студентов, являются фактором дестабилизации и вызывают существенные неравномерности в эволюции показателей успеваемости.
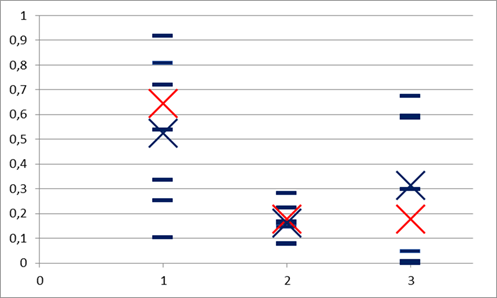
Рис. 4. Сравнение стационарных вероятностей, полученных по поэтапным значениям условных вероятностей переходов
Основные выводы
Как модель показателей успеваемости, марковская цепь НЕ ДЕМОНСТРИРУЕТ стационарность. Это можно интерпретировать как отсутствие (даже в статистическом смысле) предопределенности в учебных достижениях студентов. Учебный процесс и педагогическое взаимодействие требуют постоянных усилий с обеих сторон. В этой связи предсказание будущих результатов на основе предыдущих оказывается ненадежным и требует осторожности.

