В нечеткой математике [1] изучаются объекты самых разных типов, например, нечеткие точки, нечеткие числа, нечеткие функции. Эти объекты, или элементы, на основании некоторых свойств, которые описываются функциями принадлежности, объединяются в нечеткие совокупности, или нечеткие множества. Каждая из существующих теорий занимается изучением некоторой совокупности, или основным множеством теорий.
В нечеткой арифметике основным элементом является нечеткое натуральное число, а основным множеством – нечеткое множество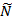 
– нечетких натуральных чисел. Это множество 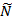может быть построено с помощью системы аксиом, которая является аналогичной системе аксиом Пеано в четкой арифметике с использованием аппарата нечеткой логики и теории нечетких множеств [1–7].
Нечеткое множество можно рассматривать как объединение его составляющих – одноточечных нечетких множеств (ОНМ), носители которых состоят из единой точки. Нечеткие множества, элементы которых – нечеткие числа, представлены в виде ОНМ, будем называть точечными нечеткими множествами (ТНМ) [4–6].
В работе [4], предлагается рассмотрение аксиоматического построения точечного нечеткого множества натуральных чисел, как основы теории точечных нечетких множеств. По нашему мнению, представляет интерес к рассмотрению аксиоматического построения теории нечетких натуральных чисел, которые представляют собой определенное объединение одноточечных нечетких натуральных чисел [4–6].
В данной работе мы предлагаем рассмотрение аксиоматического построения теории нечетких натуральных чисел как основы нечеткой арифметики.
Основные понятия теории нечетких множеств, элементов нечеткой логики, нечетких соотношений и нечетких отношений будем рассматривать как в [1–7]. Пусть заданы нечеткие множества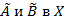 
. Введем понятие степени включения 
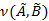нечеткого множества 
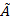в нечеткое множество 
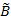, которое находится по формуле: 
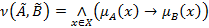, где величины 
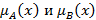понимаются как нечетко высказываемые переменные, а 
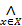– операция конъюнкции, которая берется по всем 
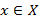. Аналогичным образом можно определить и степень включения 
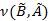нечеткого множества 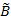в множество 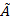. Если 
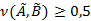, то будем считать, что множество 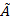нечетко включается в множество 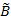и обозначается 
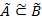. Если 
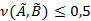, то считаем, что множество 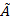нечетко не включается в множество 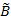и обозначается 
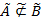. Легко увидеть, что рассмотренное понятие нечеткого включения нечетких множеств является обобщением понятия включения четких множеств. Подчеркнем, что степень включения одного нечеткого множества в другое может быть определена для любых двух нечетких множеств. При этом она может принимать любое значение в пределах от 0 до 1.
Определим степень равенства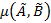 
нечетких множеств 
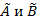выражением: 
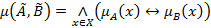. Если 
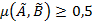, то будем считать, что множества 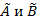нечетко равные, и определяются 
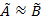. Если 
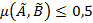, то считаем, что множества 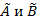нечетко не равные, и определяются выражением 
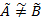. В случае, когда 
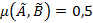, множества 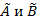одновременно нечетко равные и нечетко не равные. Эти множества называют взаимно индифферентными и обозначают 
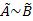. Понятно, что рассмотренное понятие степени равности двух нечетких множеств является обобщением понятия равности четких множеств 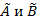, поскольку в случае 
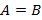имеем 
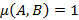, а при 
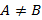получим 
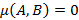. Есл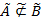и и 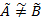, то будем считать, что 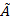нечетко строго включается в множество .
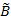Легко показать, что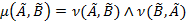 
, то есть степень равенства нечетких множеств определяется как минимум из их степеней включения. Если 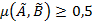, то есть множества 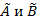нечетко равные, то 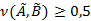и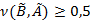 
. Так что, множество 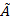нечетко включается в множество 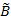и наоборот. От сюда следует метод доказательства нечеткого равенства двух и более нечетких множеств, основанный на доказательстве взаимного нечеткого включения.
Нечетким отношением на произвольном непустом множестве X называется и через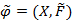 
обозначается пара множеств, в котором 
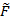является нечетким множеством в 
.
Пусть дано произвольное нечеткое отношение .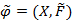
Степенью рефлективности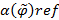 
называется величина, которая определяется выражением 
.
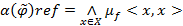Отношение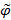 
называется нечетко рефлексивным, если 
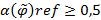. Отношение 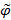называется нечетко нерефлексивным, если 
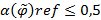. Если 
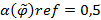, то отношение 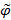называется рефлексивно индифферентным.
Степенью антирефлективности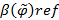 
называется величина, которая определяется следующим выражением 
.
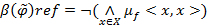Отношение 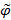называется нечетко антирефлексивным, если 
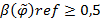и нечетко неантирефлексивным, если 
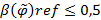. В случае, когда 
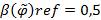, то отношение 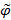антирефлексивно индифферентно.
Степенью симметричности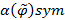 
называется величина 
.
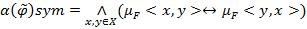Отношение 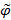называется нечетко симметричным, если 
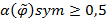. Отношение 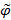называется нечетко не симметричным, если 
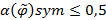. Если 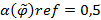, то отношение 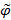называется симметрично индифферентным.
Степенью антисимметричности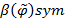 
называется величина 
.
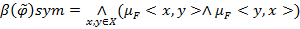Отношение 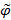называется нечетко антисимметричным, если 
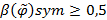и нечетко не антисимметричным, если 
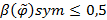. В случае, когда 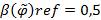, то отношение 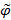называется антисимметрично индифферентным.
Степенью транзитивности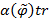 
отношения 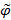называется величина 
.
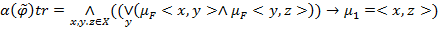Отношение 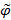называется нечетко транзитивным, если 
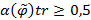и нечетко не транзитивным, если 
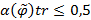. В случае, когда 
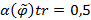, то отношение 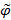называется транзитивно индифферентным.
Отношение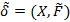 
будем называть отношением нечеткого строгого порядка, если оно нечетко антирефлексивно, нечетко антисимметрично и нечетко транзитивно. Другими словами, отношение 
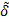является нечетким строгим порядком, если величина 
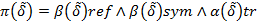, которая называется степенью строгого порядка отношения 
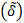, больше или равна 0,5. Если 
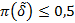то 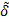не является нечетким строгим порядком. В случае, когда 
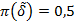, то отношение 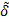будем называть индифферентным относительно строгого порядка.
Пусть 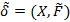– нечеткий строгий порядок на множестве X. Если 
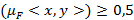, тогда говорят, что элементы 
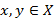связаны отношением нечеткого строгого порядка и элемент x нечетко предшествует элементу y.
Теперь нечеткое множество 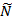– нечетких натуральных чисел, может быть построена с помощью следующей системы аксиом:
I. Нечеткий ноль – нечеткое натуральное число.
II. Всякому нечеткому натуральному числу x нечетко соответствует единое другое нечеткое натуральное число, которое называется нечетко следующим за x и обозначается x+.
III. Нечеткое число, нечетко следующее за нечетким натуральным, нечетко отличается от нуля.
IV. Нечетко отличимым натуральным числам нечетко соответствуют нечетко отличимые следующие.
V. (Аксиома индукции). Пусть множество 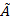, которое содержит нечеткий ноль, нечетко включено в множество 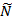и является таким, что если 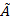содержит x, то 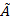содержит x+. Тогда 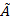нечетко совпадает с множеством .
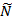Выводы. В данной работе рассмотрено применение для аксиоматического построения множества нечетких натуральных чисел нечеткой логики и теории нечетких множеств. Особое внимание приделяется рассмотрению элементов нечеткой логики, нечеткого включения, нечеткого равенства, нечеткого отношения и его основных свойств в пространстве нечетких множеств.