Во многих задачах финансово – экономической сферы могут быть полезны методы теории игр. В частности, эти методы применяются в условиях неопределенности и риска, когда поведение противоположной стороны (необязательно враждебное) просто неизвестно или известно нечетко [1]. Любая конечная матричная игра может быть решена графически (графоаналитически), либо ее решение может быть сведено к решению пары двойственных задач линейного программирования [2]. Однако в случае матричных игр, в которых элементы платежной матрицы представляют собой нечеткие числа, возникает проблема с использованием для решения таких игр симплекс – метода, связанная с делением на нечеткие числа, носитель которых содержит нуль. Эта операция над нечеткими числами не определена [3]. Графический метод применим только для игр, в которых хотя бы у одного из игроков имеется две стратегии. Однако он хорошо иллюстрирует содержательную сторону процесса поиска решения в игре и графически наглядно поясняет основные понятия теории матричных игр. В случае решения нечетких матричных игр графическим методом проблем проведения операций над нечеткими числами в основном не возникает. Неопределенность при решении нечетких матричных игр графическим методом может быть описана с использованием математического аппарата теории нечетких множеств и нечеткой геометрии [4–6].
В данной работе предлагается рассмотрение графического метода решения нечетких матричных игр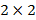 
в финансово – экономической сфере с использованием аппарата нечеткой математики и нечеткой геометрии. Основные понятия теории нечетких множеств, нечетких соответствий и отношений, понятия нечетких геометрических объектов и нечетких геометрических фигур на плоскости будем полагать такими же, как и в [4–8].
Графический метод вполне применим для нечетких матричных игр размерностью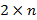 
или 
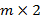, которые в свою очередь могут быть сведены к игре .
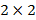Рассмотрим случай, когда задана игра размерностью 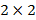с платежной матрицей:
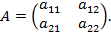
Пусть элементы матрицы A – гауссовы нечеткие числа с функциями принадлежности:
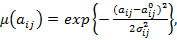где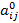 
– модальное значение (ядра) нечетких чисел, 
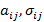– коэффициенты концентрации.
Пусть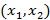 
нечеткие оптимальные стратегии игрока 1, 
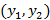– нечеткие оптимальные стратегии игрока 2. Тогда исключая тривиальный случай (наличие нечеткой чистой оптимальной стратегии хотя бы у одного из игроков), имеем:
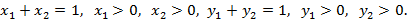(1)
Далее, для удобства, нечеткие точки, нечеткие прямые и нечеткие отрезки будем изображать графически их модальными значениями (ядрами), а их размытость (нечеткость) – крайними численными значениями коэффициентов концентрации.
Выберем прямоугольную систему координат и отложим на оси абсцисс единичный отрезок для представления нечетких смешанных стратегий игрока 1 (рис. 1). На концах этого отрезка поставим два перпендикуляра, на которых будем откладывать нечеткие выигрыши игрока, когда он использует нечеткие чистые стратеги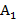и 
и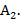 
Пусть игрок 2 выбрал нечеткую стратегию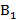 
. Тогда при использовании игроком 1 нечеткой стратегии 
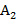он получает нечеткий выигрыш 
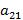(соответствующая нечеткая точка на левом перпендикуляре), а при использовании нечеткой чистой стратегии 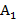– нечеткий выигрыш 
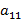(нечеткая точка на правом перпендикуляре). Соединив эти две нечеткие точки нечетким отрезком нечеткой прямой, мы получим график смешанной стратегии x при условии, что игрок 2 использует нечеткую чистую стратегию 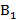(рис. 1). Точно такие же нечеткие прямые можно построить для 
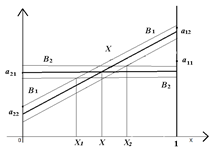
Рис. 1. График зависимости нечеткого выигрыша игрока 1 от смешанной стратегии
Нечеткая ломанная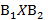 
является нечеткой нижней границей выигрыша (рис. 1) получаемого игроком 1. Нечеткая точка X в которой он максимален, определяет нечеткую цену игры и ее решение. Аналогично можно найти нечеткую оптимальную смешанную стратегию игрока 2 и нечеткую нижнюю цену игры. Согласно основной теореме матричных игр решение в нечетких смешанных стратегиях существует всегда и 
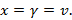Здесь v – нечеткая цена игры.
Рассмотрим использование исследуемого метода в нечетких матричных играх 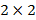на примере задач из финансово-экономической сферы.
Пример. Банк A заинтересован в покупке акций некоего акционерного общества B. Стремясь сделать покупку как можно выгодной, банк снабжает продавца информацией о реальной стоимости акций, которая может быть как нечетко правдивой
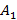, так и нечетко ложной 
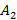. Продавец может как поверить информации
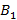, так и не поверить 
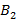с некоторой степенью истинности соответственно. Пусть в качестве платежа используется нечеткий прирост стоимости по отношению к вложенным средствам, и нечеткая платежная матрица имеет вид:
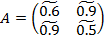, где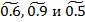 
– нечеткие гауссовы числа с следующими функциями принадлежности соответственно:
; 
; 
.
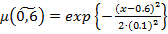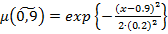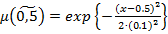Определить нечеткие оптимальные стратегии игроков A и B, а также нечеткую цену игры графическим методом.
Решение. Нечеткая нижняя цена игры: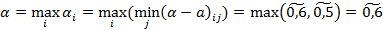 
; нечеткая верхняя цена игры: 
; 
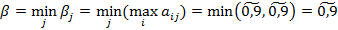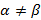; нечеткая цена игры: 
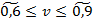. Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.
Построим на плоскости отрезки, соответствующие стратегии игрока 2 (рис. 2.а.) и игрока 1 (рис. 2.б.).
Рис. 2. Геометрическая интерпретация задачи при стратегиях игрока 2 (а) и при стратегиях игрока 1 (б).
Построив проекции нечетких точек пересечения нечетких отрезков на соответствующие оси системы координат, находим нечеткие оптимальные стратегии и нечеткую цену игры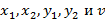 
с соответствующими функциями принадлежности:
; 
;
; 
; 
.
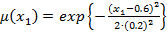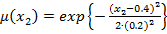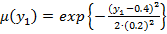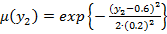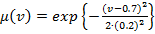Выводы. В данной работе предлагается рассмотрение графического метода решения матричных игр 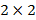, в которых элементы матрицы – гауссовы нечеткие числа. Рассмотрено использование исследуемого метода в играх 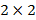на примере численного решения задач из финансово-экономической сферы.