Анализ существующих методов
Методы газовой хроматографии нашли применение не только для качественного и количественного анализа сложных углеводородных смесей, но и для измерения удельной поверхности твердых сыпучих веществ, таких как сорбенты, катализаторы, пигменты и др.
Удельная поверхность – это полная поверхность частицы с учётом пор и трещин, на единицу массы пробы. Удельная поверхность – это усреднённая характеристика размеров внутренних полостей (каналов, пор) пористого тела или частиц раздробленной фазы дисперсной системы. Данный параметр является также информативным (получение глинозема как сырья для алюминия, извлечение золота из растворов и пульп, производство цементов, катализаторов и др.), так как позволяет контролировать скорость гетерогенных процессов и управлять качеством готового продукта. Для цементов, катализаторов и сорбентов – это важный показатель качества. Чем больше, чем развитее удельная поверхность частиц, тем выше каталитическая активность или сорбционные характеристики. Для измерения удельной поверхности существует много различных методов, отличающихся друг от друга точностью, производительностью, стоимостью анализа. Первая и вторая группа методов (микроскопический и седиментационный) являются чисто лабораторными методами и неприемлемы для экспресс-анализа и автоматизации. Методы газопроницаемости просты и экспрессны, но дают информацию только о внешней поверхности частиц, без учета внутренних каналов и пор.
Статические методы основаны на определении количества поглощенного газа в зависимости от его давления, т. е. получать изотерму адсорбции. Являясь наиболее точными, статические методы довольно громоздки, весьма длительны (до 5 часов!). Время анализа зависит от дисперсности проб и в соответствии с этим может меняться от 25 до 300 мин. Диапазон измерения поверхности от 0,1 м²/г до 2000 м²/г. Относительная погрешность составляет ±2 %. Статические методы не могут применяться для технологического контроля удельной поверхности ввиду большого запаздывания информации, а используются как эталонные [1].
Наиболее пригодна для технологических измерений и автоматизации производственных процессов группа адсорбционных динамических методов измерения удельной поверхности. Динамический метод заключается в том, что поток газа или пара пропускают непрерывно через слой адсорбента, в равновесных условиях фиксируют изменение концентрации газа или пара после прохождения адсорбента. Примером динамического метода измерения удельной поверхности является метод тепловой десорбции (метод БЭТ). Этот метод предложен Нельсоном и Эггертсоном, Грубнером, усовершенствован Буяновой и Карнауховым. Метод получил широкое распространение и является достаточно чувствительным и менее длительным. Сущность метода тепловой десорбции (МТД) заключается в том, что из смеси адсорбата с газом-носителем производится поглощение адсорбата при охлаждении адсорбента до температуры конденсации [2]. Это временно приводит к уменьшению концентрации адсорбата в смеси, проходящей через измерительную ячейку катарометра, что регистрируется и отображается на мониторе в виде адсорбционного пика (рис.1). После установления адсорбционного равновесия и восстановления прежнего состава газовой смеси выходной сигнал детектора возвращается к нулевому значению. При повышении температуры адсорбента наступает десорбции адсорбата с поверхности адсорбента, концентрация адсорбата в смеси в результате возрастает [3].
Рис. 1 Графики процесса адсорбции (а) и десорбции (б) для баритового концентрата при лаздичных относительных давлениях адсорбата P/Po
Это изменение записывается на мониторе в виде десорбционного пика, направленного в противоположную сторону от нулевой линии по отношению к адсорбционному пику. В качестве адсорбата применяется азот или аргон в смеси с гелием.
Уравнением локализованной адсорбции на однородной поверхности при адсорбции в виде мономолекулярного слоя (рис.1) является уравнение Лэнгмюра:
, (1)
где 
– величина адсорбции, соответствующая полному заполнению поверхности (ёмкость монослоя), k – константа, зависящая от энергии взаимодействия и температуры.
В области малых концентраций, когда 
, уравнение 1 переходит в уравнение Генри.
При значительных концентрациях, когда , уравнение 1 превращается в уравнение 
. При этом наступает насыщение адсорбента, дальнейшая адсорбция прекращается. Таким образом, из уравнения Лэнгмюра следует, что вначале адсорбция возрастает пропорционально увеличению концентрации, затем возрастание замедляется, наконец, когда наступает предел насыщения, прекращается. Следовательно, изотерма адсорбции Лэнгмюра графически представляет собой гиперболу, обращенную выпуклой стороной от оси концентраций и асимптотически приближающуюся к пределу, соответствующему (рис. 2).
Рис. 2. Изотерма мономолекулярной адсорбции Лэнгмюра
Величина 
представляет собой количество адсорбированного вещества (в молях на грамм адсорбента), покрывающие поверхность адсорбента плотным монослоем. Эту величину называют емкостью монослоя. Зная емкость монослоя, можно определить поверхность адсорбента, если известна площадь, занимаемой одной адсорбированной молекулой:
Повышение давления газа при адсорбции может существенно изменить состояние системы и вызвать появление новых закономерностей. Так, при значительном давлении газ переходит в состояние пара, а последний при достижении давления равного давлению насыщения, конденсируется.
Адсорбционный слой при этом утолщается, адсорбция становится полимолекулярной, а изотерма адсорбции проходит черев точку перегиба и принимает форму, изображенную на рис.3. При достижении Р=Рs наступает объемная конденсация.
Рис. 3 Изотерма полимолекулярной адсорбции
При выведении уравнения изотермы полимолекулярной адсорбции принимается, что при адсорбции пара адсорбированные на уже занятых местах молекулы не покидают их немедленно, но образуют кратные адсорбционные комплексы (рис. 4).
Рис. 4 Модель полимолекулярной адсорбции по теории БЭТ
Полученное Брунауэром, Эмметом и Теллером двухконстантное уравнение полимолекулярной адсорбции (уравнение БЭТ) имеет вид:
, (2)
где а – величина адсорбции, см3/г, am – емкость монослоя в модели БЭТ, моль/г, С – энергетическая константа, связанная с теплотой адсорбции, зависит от природы сорбента, Р– равновесное давление паров адсорбата при температуре адсорбции (77 К), Р0 – упругость насыщенных паров адсорбата, Р/Р0 – относительное давление паров адсорбата [1].
Исходя из уравнения БЭТ можно определить удельную поверхность адсорбента. Для этого уравнение БЭТ преобразовывают так, чтобы зависимость адсорбции от равновесного давления паров выражалась линейным уравнением. Тогда уравнение БЭТ примет вид:
, (3)
График этого уравнения в координатах Р/Р0 и а – прямая линия. Эта прямая отсекает на оси ординат отрезок D = 1/amC, а тангенс угла ее наклона равен E = (C-1)/amC. Из величин D и E путем несложных расчетов можно вычислить константы уравнения: am и С.
Авторы теории БЭТ предложили вычислять удельную поверхность S как произведение ёмкости монослоя и площадь, приходящаяся на одну молекулу адсорбата на число Авогадро по уравнению:
, (4)
где S – площадь поверхности адсорбата; N - число Авогадро, равное 6,02•1023 шт/моль, ωm – площадь, приходящаяся на одну молекулу в монослое, равная, как показали дополнительные эксперименты, для молекулы азота 0,162 нм2, а для молекулы аргона 0,176 нм2. Расчет величины удельной поверхности по уравнению 4 с учетом размерностей всех входящих множителей имеет вид:
S = 57,5 •10-3[дм3/г]• 6,02 1023[шт/моль]• 0,162 •10-18 [м2/шт] • 22,4-1[дм3/моль]= 250 м2/г.
Рис. 5 Изотерма адсорбции азота (77К) на образце диоксида титана
Обсуждение результатов
По сравнению со статическими методами метод тепловой десорбции (БЭТ) имеет ряд существенных преимуществ, но в то же время не лишен недостатков, главными из которых являются длительность анализа (до 2,5 – 3-х часов) и обязательное наличие криостатов. Кроме того, это и необходимость тренировки образца, которая предусматривает выдержку образца в потоке газа-носителя при значительных температурах (до+200 °С). Многие образцы при таких температурах разлагаются. Альтернативой для экспресс-анализа в промышленных условиях могут служить анализаторы, работающие на основе высокотемпературного метода тепловой десорбции (ВМТД). Суть метода ВМТД заключается в определении объема адсорбата, адсорбированного на поверхности анализируемой пробы из потока парогазовой смеси при плюсовой температуре, затем десорбированного из неё при повышении температуры до 100 ºС, последующем интегрировании сигнала и расчёте удельной поверхности по программе, составленной для контроллера [3].
Сорбтометр имеет блочную конструкцию (рис. 6) и состоит из: блока подготовки воздуха (БПВ); блока адсорбера (БА); блока детектора (БД); блока измерительно-преобразующего (БИП); программно-логического контроллера (ПЛК); термостата детектора; термостата адсорбера; панели оператора (ИП); ноутбука с ПО.
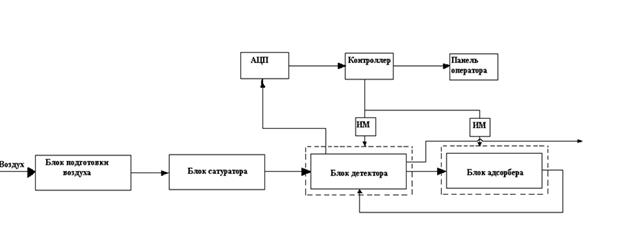
Рис 6. Структурная схема анализатора удельной поверхности (ВМТД)
Контроль процесса определения удельной поверхности производится путем подключения прибора к ПК. Пользовательский интерфейс выполнен в SCADA- Trace Mode 6. В данную систему визуализации вынесены величины температуры детектора и адсорбера, контроль объёма воздуха на выходе, время анализа, тренд адсорбции, что позволяет управлять процессом в автоматическом режиме и представлять процессы измерений в графическом виде в реальном масштабе времени. Созданный интерфейс позволяет управлять процессом (подача воздуха, нагрев) непосредственно с монитора компьютера.
Заключение
Исходя из анализа достоинств и недостатков методов измерения удельной поверхности сорбентов (статических, динамических хроматографических, газопроницаемости) по критерию времени анализа и возможности автоматического термостатирования и исключения ручных операций рекомендован хроматографический метод высокотемпературной тепловой десорбции (ВМТД).