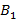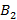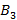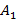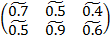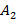Во многих задачах финансово-экономической сферы, в частности, в задачах маркетинга, менеджмента, финансово-банковских операций, инвестиций в различные проекты и др. в условиях рыночной экономики возникает необходимость принятия решения. Проблема принятия решения осложняется тем, что ее приходится решать в условиях неопределенности.
Математизация содержательных финансово-экономических задач о принятии решений в условиях неопределенности (нечеткости) приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теория четких и нечетких игр [1-4].
Любая конечная матричная игра может бать решена графически (графоаналитически), либо ее решение может быть сведено к решению пары двойственнных задач линейного программирования [1-3]. Графический метод применим только для игр, в которых хотя бы у одного из игроков имеется две стратегии. Однако он хорошо иллюстрирует содержательную сторону процесса поиска решения в игре и графически наглядно поясняет основные понятия теории матричных игр. В случае решения нечетких матричных игр графическим методом проблем проведения операций над нечеткими числами в основном не возникает. Неопределенность при решении нечетких матричных игр графическим методом может быть описана с использованием математического аппарата теории нечетких множеств и нечеткой геометрии [3-7].
В данной работе предлагается рассмотрение графического метода решения нечетких матричных игр в финансово-экономической сфере с использованием аппарата нечеткой математики и нечеткой геометрии.
Основные понятия теории нечетких множеств, нечетких соответствий и отношений, понятия нечетких геометрических объектов и нечетких геометрических фигур на плоскости будем полагать такими же, как и в [4-6].
Графический метод вполне пригоден для нечетких матричных игр размерностью m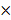
2 или 2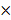n.
Рассмотрим вначале случай, когда задана игра размерностью 2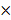n с платежной матрицей:
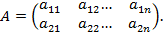
Пусть элементы матрицы A – гауссовы нечеткие числа с функцией принадлежности
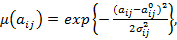где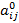 
– модальное значение (ядра) нечетких чисел 
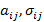– коэффициенты концентрации.
Пусть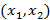 
нечеткие оптимальные стратегии игрока 1, 
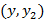– нечеткие оптимальные стратегии игрока 2. Тогда исключая тривиальный случай (наличие нечеткой чистой оптимальной стратегии хотя бы у одного из игроков), имеем:
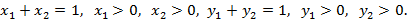(1)
Далее, для удобства, нечеткие точки, нечеткие прямые и нечеткие отрезки будем изображать графически их модальное значение (ядра), а их размытость (нечеткость) определяется численными значениями коэффициентов концентрации.
Выберем прямоугольную систему координат и отложим на оси абсцисс единичный отрезок для представления нечетких смешанных стратегий игрока 1 (рис. 1).
На концах этого отрезка поставим два перпендикуляра, на которых будем откладывать нечеткие выигрыши игрока, когда он использует нечеткие чистые стратеги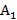и 
и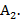 
Пусть игрок 2 выбрал нечеткую стратегию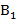 
. Тогда при использовании игроком 1 нечеткой стратегии 
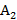он получает нечеткий выигрыш 
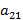(соответствующая нечеткая точка на левом перпендикуляре), а при использовании нечеткой чистой стратегии 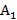– нечеткий выигрыш 
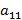(нечеткая точка на правом перпендикуляре). Соединив эти две нечеткие точки нечетким отрезком нечеткой прямой, мы получим график смешанной стратегии x при условии, что игрок 2 использует нечеткую чистую стратегию 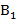(рис. 1). Точно такие же нечеткие прямые модно построить для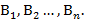 
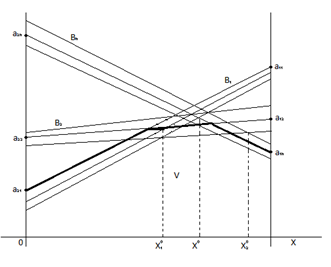
Рис. 1. График зависимости нечеткого выигрыша игрока 1 от смешанной стратегии
Далее мы должны для каждой нечеткой смешанной стратегии x, то есть для каждой точки нечеткого одиночного отрезка на оси абсцисс, найти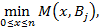 
то есть нечеткую нижнюю границу множества нечетких прямых. Эта нечеткая граница отмечена жирной нечеткой линией (рис. 1). Та нечеткая точка нечеткого отрезка, при которой нечеткая нижняя граница достигает максимума, соответствует искомой нечеткой смешанной стратегии 
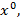высота максимума дает при этом значение нечеткой нижней цены игры при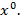 
Аналогично можно найти нечеткую оптимальную смешанную стратегию игрока 2 и нечеткую нижнюю цену игры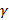 
в нечетких играх m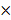2 с той лишь разницей, что здесь нужно искать не максимум нечеткой нижней границы, а минимум нечеткой верхней границы.
Согласно основной теореме матричных игр решение в нечетких смешанных стратегиях существует всегда и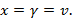 
Здесь v – нечеткая цена игры.
Рассмотрим использование исследуемого метода в нечетких матричных играх на примере задач финансово-экономической сферы.
Пример. Рассмотрим две конкурирующие финансовые компании А и В. Компания В ведет переговоры с организаторами каждого из трех проектов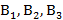 
на предмет инвестирования. Задача компании В: положительный результат переговоров. Компания А ставит своей задачей свести переговоры компании В к отрицательному результату с тем, чтобы занять место компании В в инвестировании.
Компания А для достижения своей цели – срыва переговоров компании В может применить одно из двух средств: стратегия 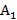– предложить организаторам проектов более выгодные условия инвестирования по сравнению с компанией В и стратегия 
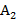– представить в распоряжение организаторов проектов материалы, компрометирующие компанию В.
В качестве выигрыша игрока А (или проигрыша игрока В) рассмотрим нечеткую вероятность отрицательного результата переговоров компании В. В соответствии со своими задачами игрок А стремится максимизировать выигрыш, а игрок В – минимизировать.
Матрица игры с нечеткими показателями эффективности стратегий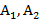 
и нечеткими показателями неэффективности стратегий 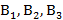имеет следующий вид:
|
|
|
|
|
|
|
|
||
|
|
|||
где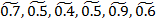 
– нечеткие гауссовы числа с соответствующими функциями принадлежности:
, 
, 
,
, 
, 
.
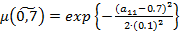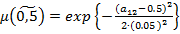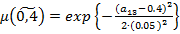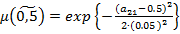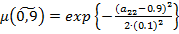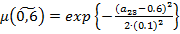Решим поставленную задачу изложенным выше графическим методом.
Нижняя цена игры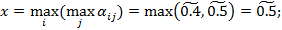 
верхняя цена игры
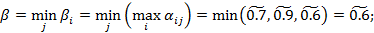цена игры: 
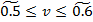. Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегии игрока 1 (рис. 2а) и игрока 2 (рис. 2б).
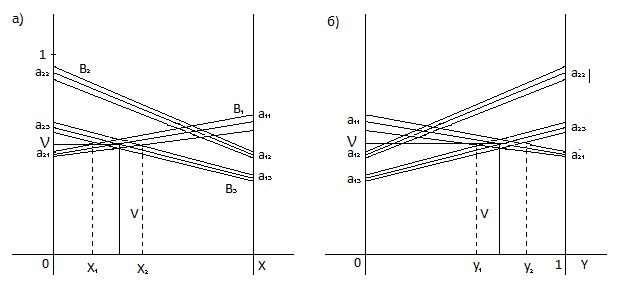
Рис. 2. Геометрическая интерпретация задачи при стратегиях игрока 1(а) и при стратегиях игрока 2(б).
Построив проекции нечетких точек пересечения нечетких отрезков на соответствующие оси системы координат, находим нечеткие оптимальные стратегии и нечеткую цену игры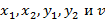 
с соответствующими функциями принадлежности:
; 
; 
;
; 
.
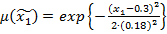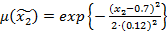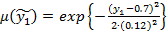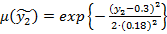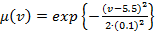Выводы. В данной работе предлагается рассмотрение графического метода решения матричных игр, в которых элементы матрицы – гауссовы нечеткие числа. Вначале рассмотрен случай, когда задана игра размерностью 2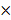n. Случай, когда задана игра размерностью m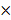2, рассматривается аналогично. Рассмотрено использование исследуемого метода в играх размерностью 2n на примере численного решения задач из финансово-экономической сферы.