В школьном курсе алгебры 9 класса, в связи с изучением теории вероятности появляется необходимость в изучении комбинаторики. Естественным образом из определения вероятности вытекает необходимость перебора всех возможных вариантов. К сожалению, в школьном курсе не так много часов уделяется на изучение комбинаторики. Многие формулы даются просто как факт. Такую информацию трудно понять и, как следствие, запомнить.
Для решения этой проблемы школьникам предлагается попробовать самим вывести эти формулы.
Классической и простейшей задачей комбинаторики является задача на количество вариантов перестановок из n элементов по n позициям. Ее решение незамысловато.
Пример 1. Сколько существует вариантов расположения 6 книг на полке? Первый элемент можно разместить по 6 позициям 6 способами, второй 5 способами и так далее. Следовательно, количество вариантов (N) можно будет подсчитать следующим образом:
N=6*5*4*3*2*1=6!=720 (1)
Не сложно догадаться, что данную задачу можно обобщить. Количество перестановок из n элементов по n позициям будет находиться по формуле:
N=n!
Пример 2. Сколько различных слов можно составить из букв слова «трактат»?
Решение. Всего букв 7, причем есть 3 буквы «т» и 2 буквы «а», значит среди наших вариантов будут одинаковые. Этот факт сокращает количество различимых вариантов.
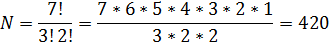
В общем случае формула будет выглядеть следующим образом:
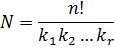
где kr –количество одинаковых (неразличимых) элементов в группе.
На практике часто число размещаемых элементов m меньше n (числа возможных позиций размещения) так появляется формула числа размещений без повторений:
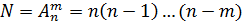(2)
То есть, мы расставляли книги по местам, а они взяли и закончились, а места для них еще остались. Поэтому цепочка множителей в формуле (1) обрывается и получается формула (2). Следовательно, количество размещений из m элементов по n возможным позициям, всегда меньше количества перестановок из n элементов по n позициям.
Как и в случае перестановок возможны размещения без повторений и с повторениями. Во втором случае количество размещений обозначается А с чертой сверху и дается другой формулой:
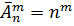
(то есть, возможность повторения увеличивает количество возможных вариантов)
Важно подчеркнуть, что всегда надо четко понимать с каким видом перестановок мы имеем дело (с повторением или без), так как формулы, им соответствующие, различны.
Перестановки и размещения описывают класс задач, в которых важен порядок расположения элементов или порядок, в котором элементы извлекались. Таких задач сравнительно немного. В реальности возникает гораздо больше задач, когда этот порядок не важен, а важен только конечный результат. Допустим, когда вы вытягиваете шары разных цветов из урны, то вам, как правило, неважно в каком порядке они появлялись, а важно, сколько шаров какого цвета появилось в конечном итоге.
Пример 3. Сколькими способами можно составить букет из пяти различных цветов, если имеется 10 различных цветов?
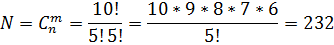
Классический пример – составление букета из m цветов, когда в распоряжении имеется их n штук.
Такие ситуации описываются числом сочетаний из n элементов по m, и для подсчета числа вариантов без повторений используется формула:
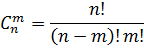
Эта формула для числа возможных сочетаний (в отличие от размещений порядок не важен)
Типичным примером сочетаний с повторениями может служить задача о покупке пирожных.
Пример 4. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами можно купить 7 пирожных?
Положим пирожные в коробку, а чтобы они не перепутались, разделим их картонными разделителями. Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.
Итак, два класса объектов 1 (7 штук) и 0 (3 штуки) — покупка — 10 объектов.
Два способа рассуждения:
(1) задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов.
(2) другой способ рассуждения (эквивалентный). Надо разбить 10 мест на две группы: для 7 пирожных и 3 разделителей.
В любом случае получается ответ:
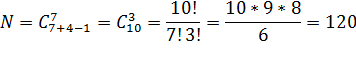
В чем особенность: объекты повторяются, причем один эклер на вкус неотличим от другого. Отсюда название: сочетания с повторениями. Можно представлять себе, что пирожные непрерывно пекут, так что они не переводятся, сколько ни ешь. Это совсем другая ситуация, чем в обычных сочетаниях.
И опять выплывают нюансы с повторениями. Если возможны повторения, то число возможных сочетаний с повторениями обозначается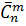 
и дается менее известной формулой :
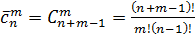[1]
Все вышеперечисленные формулы являются как бы элементарными блоками, из которых строятся решения более сложных комбинаторных задач.
Связующими элементами выступают правила сложения зависимых и независимых вариантов.
Пример 5. В секции бадминтона 10 мальчиков и 15 девочек. Сколькими способами можно сформировать команду на соревнования, если в нее должны входить два мальчика и две девочки.
Решение. Мальчиков можно выбрать С102 способами, девочек С152 способами. Всего вариантов будет:
,
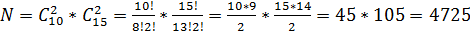Более сложные задачи комбинаторики, как правило, опираются на построение различных моделей задач с использованием сумм и произведений перестановок, размещений и сочетаний, логическое «и» соответствует произведению, а логическое «или» сумме возможных вариантов [2]. Для наглядности рассмотрим простенькую задачу:
Пример 6. Даны две параллельные прямые. На одной лежит 12 точек, на второй – 15. Сколько различных треугольников можно построить?
Решение. Две вершины должны лежать на одной прямой, третья на другой (в противном случае треугольника не получится). Поэтому количество треугольников с основанием на прямой с 12 точками будет равно:
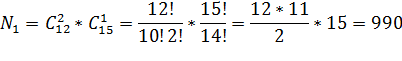
Аналогичные рассуждения для треугольников с основанием на прямой с 15 точками дают еще:
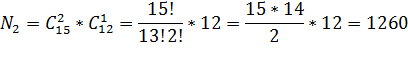
Так как эти два множества треугольников независимы, то окончательный ответ равен их сумме:
N=N1+N2=990+1260=2250
Эта задача является простым примером одновременного использования правил умножения и сложения сочетаний.
Пример 7. Рассматриваются все пятизначные числа. Сколько существует чисел, у которых цифры расположены в порядке возрастания?
Решение. Задача решается достаточно просто при правильном подходе.
Пусть в числе на первом месте стоит единица (ноль на первом месте стоять не может). Тогда оставшиеся четыре места можно заполнить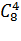 
способами (из 10 цифр мы не можем использовать 0 и 1, а выбранные четыре цифры мы всегда сможем расположить в порядке возрастания!), если на первом месте стоит двойка, то незадействованных цифр остается семь:10 –(012) и вариантов 
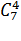и так далее. И сразу получаем правильный ответ:
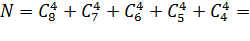70+35+15+5+1=126
Причем, не надо беспокоиться, что некоторые варианты посчитаны по нескольку раз. Другими способами эта задача решается далеко не так просто. Это, кстати, большая проблема во многих задачах – не посчитать несколько раз одни и те же варианты.
Данный материал может быть использован опытным педагогом как фрагмент урока по теме «Комбинаторика» или «Теория вероятности». При дополнении материала типовыми задачами можно построить факультативное занятие.