В системах добычи, транспорта и хранения газа и нефти запорная арматура играет исключительно важную роль в обеспечении надежности систем на всех режимах функционирования. В процессе эксплуатации конструктивные элементы трубопроводных систем различного назначения находятся под действием широкого спектра нагрузок и воздействий, обуславливающих сложные процессы трения, износа, усталости и старения. Несмотря на систематические совершенствования конструкций запорной арматуры решение проблемы обеспечения их работоспособности все еще не отвечает современным требованиям надежности и безопасности трубопроводных систем.
Одним из наиболее распространенных типов запорной трубопроводной арматуры, устанавливаемой на магистральных и технологических трубопроводах для полного перекрытия потока рабочей среды, являются задвижки. Запирающий элемент перемещается в задвижках возвратно-поступательно, перпендикулярно направлению потока рабочей среды и имеет два крайних рабочих положения - "открыто" и "закрыто".
Большой ущерб народному хозяйству и окружающей среде могут нанести потери нефти и нефтепродуктов вследствие аварий. Аварийные потери вызываются несоблюдением строительных норм и правил при проектировании и сооружении средств транспорта и хранения, нарушением правил технической эксплуатации и несвоевременным ремонтом оборудования Транспортировка нефти и полученных продуктов к потребителю связана со значительными их потерями. Потери от утечек при трубопроводном транспорте приводят к затратам общественного труда и снижению эффективности производства. Кроме того, потери нефти и нефтепродуктов при авариях, разливах и утечках загрязняют почву, грунтовые воды и водоемы. Помимо потерь ценных нефтепродуктов и загрязнения окружающей среды, утечки представляют опасность крупных аварий; взрывов и пожаров.
В настоящее время производится огромное количество конструктивных разновидностей задвижек, отличающихся конструкцией запирающего элемента (затвора), способом подсоединения к трубопроводу, расположением ходового узла, типом привода.
Правильный выбор конструкции задвижек в значительной степени предопределяет безаварийную и безотказную работу как отдельных технологических блоков в целом, так и трубопроводов в частности.
При установке запорной арматуры на трубопроводе предпочтение следует отдавать конструкциям с малым гидравлическим сопротивлением. Малое гидравлическое сопротивление задвижек делает их особо ценными при применении на трубопроводах, через которые постоянно движется среда с большой скоростью [4].
Из многообразия видов высокой герметичностью, невысоким гидравлическим сопротивлением и простотой конструкции можно выделить класс клиновых задвижек. Из недостатков клиновых задвижек следует отметить невысокую ремонтопригодность при износе уплотнительных материалов.
Отличными эксплуатационными свойствами зарекомендовала себя задвижка стальная ЗКЛ2 100-16. Это обусловлено в первую очередь её конструктивными особенностями и использованием современных высококачественных материалов. Особенность данной модели - равноценная возможность установки в вертикальном и наклонном положении.
Для оценки работоспособности необходимо определить критерии герметичности и прочности.
Поскольку корпус задвижки имеет сложную геометрическую форму, то он не может быть рассчитан методами сопротивления материалов. В тех случаях, когда аналитическое решение получить не удается, в прежде всего это касается деталей со сложной геометрической конфигурацией, используют приближенные численные методы теории упругости. Среди таких методов к настоящему времени наиболее разработаны и применяются в расчетной практике следующие: метод конечных разностей (МКР), метод конечных элементов (МКЭ) и метод граничных элементов (МГЭ). МКР основан на замене дифференциальных уравнений соответствующими уравнениями в конечных разностях, записанных на регулярной сетке [5]. Данный метод не получил широкого распространения из-за трудности описания сложных криволинейных контуров деталей. МКЭ – наиболее общий метод численного решения физических задач, описываемых при помощи дифференциальных уравнений в частных производных. С помощью МКЭ также решаются задачи смазки и теплопроводности, анализируются колебания систем, решаются задачи электростатики, движения жидкости по трубам. Он применяется для анализа напряжений и деформаций несущих конструкций и деталей практически любой техники.
Основное уравнение метода конечных элементов является системой линейных уравнений, неизвестными которой являются узловые перемещения [2]:
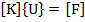. (1)
Корпуса запорной арматуры проходят в обязательном порядке гидравлическое испытание при приложении двойного рабочего давления. Для данной задвижки оно равно 3,2 МПа [3].
Согласно анализу, проведенному в работе [1], был сделан вывод, что из всех существующих на данный момент промышленных пакетов наиболее точным и универсальным является ANSYS.
Конечно-элементный анализ состоит из 5 этапов:
1) Построение геометрии в SolidWorks.
Импортирование модели через формат ACIS.
2) Построение конечно-элементной сетки.
Для разбивки был выбран конечный квадратичный элемент SOLID186, так как он хорошо описывает криволинейные поверхности. Параметры материала были заданы следующими. Чтобы обеспечить удовлетворительное качество сетки размер элемента был выбран 10мм [7].
3) Задание граничных условий.
Поскольку модель является симметричной относительно 2-х плоскостей, то анализу подверглась только 1/4 модели. На плоскостях разреза были указаны условия симметрии. Опора задвижки жестко заделана. По всей внутренней поверхности корпуса задвижки указано внутреннее давление 1,6 МПа.
4) Для решения задачи использовался прямой решатель SPARSE SOLVER, именно он используется в ANSYS по умолчанию.
5) Анализ результатов.
Оценка качества конечно-элементной сетки осуществлялась по формуле:
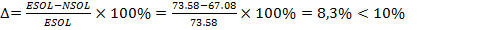(2)
Поскольку значение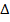 
меньше 10%, то качество сетки можно считать удовлетворительной [6].
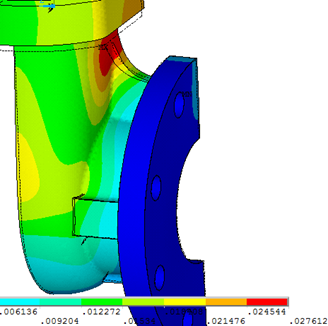
На рисунке 1 представлены картины распределения суммарных перемещений ЗКЛ2 100-16. Для наглядности деформация преувеличена в 300 раз.
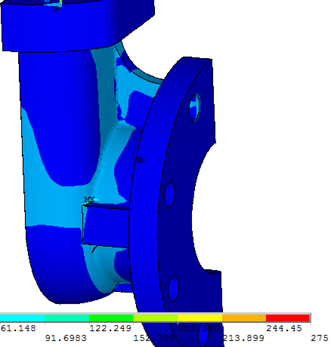
На рисунке 2 показаны распределения эквивалентных напряжений по Мизесу. Максимальное значение составляет 67,083 МПа, что не превышает предел текучести материала 275 МПа, чем обеспечивается прочность детали.
Выполняя моделирование разных вариантов нагружения, установим зависимость эквивалентных напряжений от приложенного давления.
Для решения задачи полиномиальной регрессии был выбран универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов MathCAD. Это программное средство объединяет в себе простой текстовый редактор, математический интерпретатор и графический процессор.
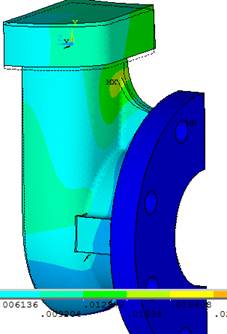
а б
Рисунок 1. Распределение суммарных перемещений.
а) перемещения в случае приложения давления в 3,2 МПа,
б) - критического давления в 5 МПа.
а б
Рисунок 2. Распределение эквивалентных напряжений по Мизесу.
а) напряжения в случае приложения давления в 3,2 МПа,
б) - критического давления в 5 МПа.
В математическом процессоре MathCad аппроксимируем полученные результаты полиномиальной регрессии.
Установленная зависимость выглядит следующим образом:
Stress(x) = - 0.0001311•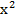
+50.487692• x - 0.002385 (3)
Она изображена на рисунке 3.
Приравнивая функцию (3) к величине предела текучести, мы получаем квадратное уравнение, решая которое, определяем предельное давление, которое может выдержать данный корпус P=5,447МПа.
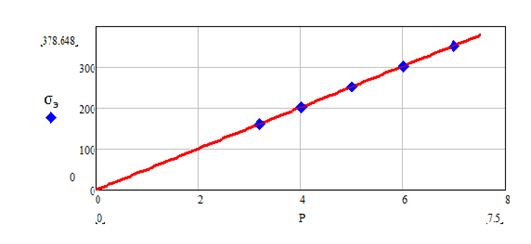
Рисунок 3. Восстановленная функция напряжений от приложенного давления