Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Современная экономическая ситуация в России характеризуется усложнением организационной структуры производства, углублением общественного разделения труда, развитием торговой индустрии. В этих условиях существенно возрастают требования к методам планирования и хозяйственного руководства. Широкое применение в менеджменте организаций находят теория и методы экономико-математического моделирования, позволяющие формировать систему целей, строить текущие и перспективные планы, оптимизировать их обеспечение необходимыми ресурсами, принимать эффективные управленческие решения.

В условиях рыночной экономики особое внимание математиков и экономистов привлекает разработка методов совершенствования деятельности торговых предприятий, представляющих собой независимые хозяйствующие субъекты, осуществляющие закупку, хранение, реализацию товаров с целью получения прибыли и удовлетворения потребностей рынка. Организация эффективной деятельности торгового предприятия способствует созданию устойчивых связей между экономическими контрагентами – от производителя до конечного потребителя [4].

В то же время анализ работ в области экономико-математического моделирования показывает, что проблемы планирования деятельности торговых предприятий остаются малоизученными. Большинство математических моделей, разработанных в сфере коммерческой деятельности, относятся к производственным организациям. При этом вопросы оптимизации рассматриваются не в комплексе, а по отдельным этапам и сферам деятельности: оптимизация инвестиционной политики, управление оборотным капиталом, планирование производственной мощности предприятия, управление запасами, эффективное использование трудовых ресурсов, составление оптимальных маршрутов, расписаний и др.

Недостаточная разработанность проблемы выявления совокупности экономико-математических методов оптимизации деятельности торгового предприятия в условиях рыночной экономики определяет актуальность темы исследования. Предметом исследования выступают модели и методы линейного и динамического программирования как инструментальные средства оптимизации деятельности торгового предприятия.

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. В данной статье рассматривается математический подход к решению задачи оптимального управления запасами. Возникновение задач этого типа связано с работами Ф. Эджуорта и Ф. Харриса, появившимися в конце 19 − начале 20 века, в которых исследовалась простая оптимизационная модель для определения экономичного размера партии поставки для складской системы с постоянным равномерным расходом и периодическим поступлением хранимого продукта [5].

Запасом называется любой ресурс, который хранится для удовлетворения будущих нужд. Примерами запасов могут стать полуфабрикаты, готовые изделия, материалы, различные товары, а также денежная наличность, находящаяся в хранилище. Причинами создания запасов являются дискретность поставок, случайные колебания спроса за период между поставками, объема поставок, сезонность спроса или производства. Существуют также причины, побуждающие предприятия минимизировать запасы: плата за хранение, физические потери при хранении; моральный износ продукта [3].

Рассмотрим предприятие, производящее партиями некоторые изделия. Предположим, что оно получило заказы на п месяцев, причем размеры заказов меняются от месяца к месяцу, поэтому иногда целесообразнее выполнить одной партией заказы нескольких месяцев и затем хранить изделия, пока они не потребуются. Необходимо составить план производства на указанные месяцы с учетом затрат на производство и хранение.

Введем обозначения:

и_i − число изделий, производимых в j-й  месяц;

x_j − величина запаса к началу j-го месяца;

d_j − число изделий, отгружаемых в j-м месяце;

f_j(x_j+1,u_j) − затраты производство и хранение изделий в j-м месяце.

Считаем, что величины запасов к началу первого месяца х1 и к концу последнего хn+1 заданы. Задача состоит в том, чтобы найти план производства

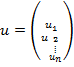(1)

компоненты которого удовлетворяют условиям баланса

x_j+u_j-d_j=x_j+1,  j=1,2,…, n            (2)

и минимизируют суммарные затраты за весь планируемый период

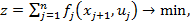(3)

При этом 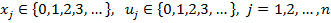(4)

Заметим, что для любого месяца j величина xj+1 запаса к концу месяца должна удовлетворять ограничениям

0≤x_j+1≤d_j+1+d_j+2+…+d_n,                                (5)

т. е. объем производимой продукции иj на этапе j может быть настолько велик, что запас xj+1 удовлетворяет спрос на всех последующих этапах, но нет смысла иметь xj+1 больше суммарного спроса на всех последующих этапах. Кроме того, управление uj должно удовлетворять ограничениям

0≤u_j≤d_j+x_j+1     (6).

Рассмотрим общее решение данной задачи методом динамического программирования, взяв за основу алгоритм, представленный в [2].

За параметр состояния х примем наличный запас в конце k-го месяца х=хk+1, а функцию состояния Fk(x) определим как минимальные затраты за первые k месяцев при выполнении условия (5):

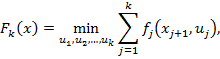
где минимум берется по неотрицательным целым значениям и1, и1...,ик, удовлетворяющим условиям

x_j+u_j-d_j = x_j+1,

x_k+u_k-d_k=x    (7)

Учитывая, что

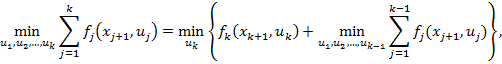
и величина запаса хk к концу (k−1)-го периода, как видно из уравнения (7), равна х_к = x+d_k-u_k  приходим к рекуррентному соотношению

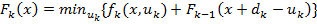
где минимум берется по переменной и_к, которая, согласно (6), может изменяться в пределах 0≤u_k≤d_k+x, причем верхняя граница зависит от значений параметра состояния, изменяющегося в пределах 0≤x≤d_k+1+d_k+1+…+d_n , а индекс k может принимать значения k=2,3,4,…, n.

При k = 1

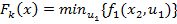, где

u₁=x+d₁-x₁, 

0≤x≤d₂+d₃+…+d_n ,

т. е. на начальном этапе при фиксированном уровне x1 исходного запаса каждому значению параметра х отвечает только одно значение переменной u₁.

Применив вычислительную процедуру динамического программирования на последнем шаге (k=n), находим значение последней компоненты и^*_n оптимального решения, а остальные компоненты определяем как

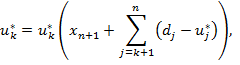
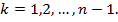
В качестве конкретного примера рассмотрим деятельность предприятия по производству полуфабрикатов в течение N календарных этапов планирования (месяцев). Каждый n-й этап характеризуется следующими параметрами:

i_n?1 ? величина запаса, оставшаяся на предприятии после окончания предыдущего n?1 -го этапа;

х_n ? объем производства предприятия на n-м этапе;

d_n ? величина спроса на продукцию предприятия на n-м этапе.

Известна функция затрат сп на п-м этапе функционирования предприятия, зависящая от объема хn производства и величины запасов in-1, которые должны храниться на складе в течение n-го периода.

Необходимо определить объем производства для каждого этапа планирования, при котором суммарные затраты, связанные с производством продукции и ее хранением, были бы минимальны, и в каждом периоде выполнялось ограничение на спрос продукции со стороны потребителей.

Критерий оптимальности представляется в виде:

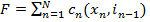→ min.

Ограничения:

1) удовлетворение спроса потребителей на продукцию в n-м периоде

d_n ≤ i_n-1 + x_n,     n = 1,¯N;

2) объем запаса в конце n-го периода

i_n =i_n-1 + x_n – d_n  ,    n= 1_,¯N,    i_n =0,¯i_max ,      х_n =0,¯х_тах .

Функциональное уравнение Беллмана имеет вид:

f_n (i_n)= min_xn (f_n-1 (i_n?1) + с_n(х_п, i_n?1)).

Рассмотрим решение уравнения Беллмана для случая, когда  c_n(x_n, i_n?1)=c_n(x_n)+h•i_n?1,

где с_n(х_n) затраты на производство продукции на n-м этапе в объеме хn,

h•i_n?1 ? затраты на хранение продукции на n-м этапе, h ? коэффициент;

i₀ ? начальный запас продукции;

c₀(i₀) ? затраты на его создание;  

h•i₀  ? затраты на его хранение.

Решим рассматриваемую задачу для следующих исходных данных:

• количсество интервалов планирования (месяцев) N=3;
• величина спроса на полуфабрикаты постоянна для всех этапов:

d1 =d2 = d3 = 400 кг/ мес.;

• затраты на формирование начального запаса с0(x0) = 90·i0; (коэффициент 90 складывается из 70 руб./кг – себестоимость одного килограмма полуфабрикатов ? и 20 руб./ кг идут на заработную плату работников;
• затраты на производство и хранение продукции

с_п (х_п,i_n?1) =12000+70· х_n +10• i_n-1;

(12000 руб. – месячный расход на заработную плату, 70 руб./кг – себестоимость одного килограмма продукции, 10 руб./кг – стоимость хранения 1 кг продукции в месяц, т.е. затраты на оплату электроэнергии, потребляемой морозильными камерами, а также на текущий ремонт оборудования);

• ограничение на производственные мощности хтax = 600 кг/мес;
• ограничение на предельный уровень запасов iтах= 400 кг/мес.

Шаг 1. Решение уравнения Беллмана производится в соответствии с алгоритмом прямой прогонки:

 f₁(i₁)=min(c₁(x₁)+c₀(i₀)+h•i₀),

i₁= x₁+ i₀?d₁.

Для решения этого уравнения формируется таблица 1, в которой столбцы соответствуют величине начального запаса, строки ? объему производства на первом этапе х1. Каждая клетка таблицы делится на две части: в нижней части записываются значения состояния в конце первого этапа (значения для переменной i₁): i₁=i₀+x₁–d₁.

Если i1 отрицательно, то такие состояния являются недопустимыми и исключаются из рассмотрения. В частности, для положительного спроса d1 > 0 клетка с х1=0 и i0=0 является недопустимой. Клетки, соответствующие недопустимым состояниям, отмечаются символом * [6].

В верхней части каждой из клеток записывается значение функции

f* (i₁) = c₁(x₁) + c₀(i₀) + h•i₀.

Приведем вычисление ряда функций f1*(i1):

f1* (0) = c1(0) + с0(400) + 10•400 = 0 + 90•400 + 4000 = 40000,

f1* (0) = c1(100) + с0(300) + 10•300 = 12000 + 70•100 + 90•300 + 3000 = 49000,

f1*(100) = c1(100)+с0(400) +10•400 =12000 + 70•100 + 90•400 + 4000 = 59000,

f1*(0) = c1 (200) + с0(200) + 10•200= 12000 + 70•200 + 90•200 + 2000 = 46000,

f1* (100) = c1(200) +с0(300) +10•300 =12000 +70•200 + 90•300 +3000 = 56000,

f1*(200) = c1(200) + с0(400) +10•400 = 12000+70•200 + 90•400 +4000 = 66000.

Таблица 1

Расчетная таблица для шага 1

Среди допустимых клеток находятся клетки с одинаковыми значениями состояний, в качестве оптимальной выбирается клетка, для которой f* (i1) принимает минимальное значение, т.е. f(i1) = min{f*(i1)}. Для каждого состояния фиксируется оптимальный объем производства х1. Результаты представляются в окончательной таблице для первого шага: в первом столбце приводится перечень состояний, во втором ? оптимальный объем производства для каждого из состояний; в третьем ? оптимальные затраты на производство и хранение запаса для первого календарного периода. Максимальное значение состояния первого этапа ограничивается imax, т.е. i1= imax , а минимальное ? i1=0.

Итоговая таблица для шага 1

Аналогичные действия выполняются для всех этапов, пока n не достигнет значения N.

Для нахождения оптимальных объемов производства хn и оптимальных уровней запаса in производим решение задачи в обратном порядке:

i₃ = 0,  х₃ = 0; i₂ = 400, х₂ = 600; i₁=200, x₁ = 600; i₀ = 0.

Вывод: для минимизации затрат на производство и хранение продукции, предприятию следует в первые два месяца производить на максимальной мощности, а в третьем месяце – только реализовать имеющиеся запасы. Такой режим работы может повторяться неоднократно.