Введение.
Методы извлечения признаков или биомаркеров из данных МРТ-изображений мозга часто начинаются с автоматического сегментирования областей интереса. Очень популярный метод сегментации - это использование распространения меток, которое преобразует метки из изображения в атласе в невидимое целевое изображение путем выравнивания обоих изображений. Атласы обычно, но не обязательно, маркируются вручную. Точность распространения меток сильно зависит от точности выравнивания базового изображения. Успешно используется сегментация меток в сочетании со слиянием при принятии решений для сегментирования большого количества структур на МР-изображениях мозга[1]. Начальный набор используемых атласов состоит из 30 атласов от молодых и здоровых субъектов. Предложенный метод используется для распространения этого начального набора атласов до 796 базовых изображений ADNI. Результаты показывают, что этот подход обеспечивает более точную сегментацию, по крайней мере частично, из-за связанного с этим уменьшения ошибки регистрации между субъектами.
Многоуровневое обучение. Набор изображений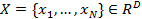 
описывается N изображениями xi, каждое из которых определяется как вектор интенсивностей, где D - количество вокселей на изображение или область (обычно D>1000000 для МР-изображений мозга). Предполагая, что xi,…,xn лежат на или вблизи d-мерного многообразия M, включенного в RD , можно изучить низко размерное представление 
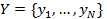с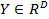 
входных изображений в M входных изображений.
Во многих описанных методах матрица обычно используется для представления отношений между парами элементов данных, которые в данной работе можно считать изображениями[2]. Матрица, в свою очередь, может рассматриваться как представляющая график для моделирования данных, в которых каждый узел является изображением, а вес каждого края обозначает сходство или несходство между парами изображений, к которым он относится. Существует широкое различие между методами, которые используют полный граф для моделирования отношений между данными и теми методами, которые используют более разреженное представление с меньшим числом ребер, ограниченным локальными окрестностями. Все приведенные ниже методы направлены на оптимизацию некоторой формы целевой функции через матричное представление. Методы описываются как спектральные, так как оптимизация часто выполняется с использованием собственной структуры собственного вектора соответствующей матрицы.
Схематический обзор метода коллективного обучения приведен на рисунке 1.
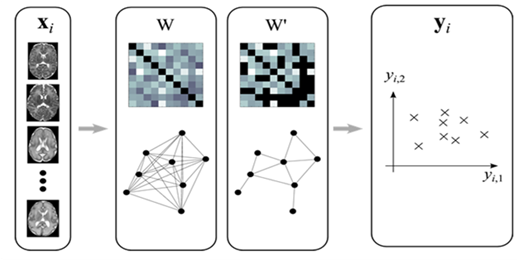
Рисунок 1. Метод коллективного обучения.
На приведенной выше схеме показаны изображения xi, 1 ≤ i ≤ N сравниваются в парах и измерениях сходства или расстояния между ними. Меры определяют матрицу N×N представляющую веса ребер в представлении графа данных. Представление графика / матрицы может быть либо полным(плотным, превышающим W), либо разреженный (W’), иллюстрации обоих случаев показаны выше. Как правило, собственных значений структуры матрицы (или матрицы, полученной из нее)используется для получения координатного представления для вложенного представления многообразия yi оригинальных данных. Первые два измерения yi схематически показаны выше.
Основной компонентный анализ (ОКA) [3] - популярный и широко используемый метод уменьшения линейной размерности. ОКA стремится описать большую часть дисперсии данных, используя несколько основных компонентов. Проблема описана как определение функции линейного отображения M, которая оптимизирует целевую функцию
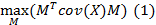
где cov(X) - образец ковариационной матрицы X. Линейное отображение определяется первыми d собственными векторами собственной задачи
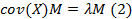
Отсюда отображение в низко размерное пространство определяется как Y = XM.
Kernel ОКА [4] - нелинейное расширение классического ОКA. Ядровая матрица K определяется из точек данных в D-мерном пространстве
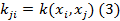
где κ может быть любой функцией, которая приводит к положительно-полуопределенному К. Центрирующая операция выполняется впоследствии, чтобы определить нулевые, средние и вычислительные функции d главных собственных векторов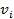 
и собственных значений 
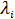из K ,и привести к собственным векторам соответствующей ковариационной матрице:
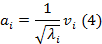
Тогда низко размерное вложение изображения xi определяется как
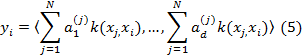
где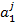 
- j-я запись вектора 
.
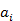Многомерное масштабирование (ММ) [5] представляет собой линейный метод, тесно связанный с ОКA. Он основан на матрице расстояний D с dij, представляющей расстояние между двумя высоко размерными элементами данных xi и xj, ММ стремится найти низко размерное представление, что наилучшим образом сохраняет попарные расстояния в многомерном пространстве. Это выполняется путем минимизации целевой функции
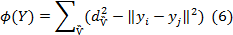
с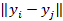 
, являющимся расстоянием между двумя точками данных в d-мерном пространстве, d<<D. Оптимальное вложение для этой целевой функции можно получить через сингулярное разложение матрицы Грама K=XXt, которое может быть получено из матрицы расстояний D.
Isomap. Isomap - это метод нелинейного внедрения, основанный на методе ММ. В Isomap парные расстояния dij не измеряются непосредственно между элементами данных Xi и Xj, но изменяются на графе окрестности G, соединяющем все N элементов данных. Этот граф определен либо путем соединения каждого элемента данных Xi с его ближайшими соседями, либо со всеми субъектами в пределах некоторого фиксированного радиуса.[6].
После построения G расстояния dij оцениваются как кратчайшие расстояния dijG в графе. Окончательные координаты вложения yi получаются применением классической ММ к матрице расстояний DG={dijG}.
Низко размерное многообразие, построенное с локально линейным вложением (ЛЛВ) [7] метод направлен на сохранение локальных районов высоко размерных данных в низко размерное пространство. Метод предполагает локально линейную зависимость между соседними точками данных. Идея состоит в том, чтобы представлять каждый элемент данных Xi как взвешенное сочетание его k ближайших соседей в высоко размерном пространстве. Это определяется множеством весов Wij для k соседей Xi и цель состоит в том, чтобы найти низко размерное представление yi, которое учитывает это взвешивание. Объектная функция ЛЛВ определена в виде
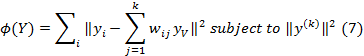
С малой весовой матрицей W вложение получается из d собственных векторов соответствующих наименьшим ненулевым собственным значениям (I-W)T(I-W).
Используя ту же концепцию локальной линейности, что и ЛЛВ, Гессенское ЛЛВ [8] минимизирует кривизну многомерного многообразия при изучении низко размерного представления. Метод обеспечивает локальную изометрию между расстояниями в обоих пространствах. Применение ОКA к каждой точке данных Xi и его k ближайшим соседям дает приближение локального касательного пространства в каждой точке данных. Полученная отображающая функция M от d главных компонент в каждой точке Xi затем используется, чтобы дать оценку для гессиана Hi многообразия в этой точке данных. Из оценок Гессиана в касательном пространстве матрица H строится с элементами
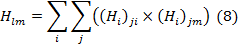
Собственные векторы, соответствующие d наименьшим собственным векторам H, используются для определяют низко размерного вложенияY, минимизирующего кривизну многообразия.
Применение многоуровневого обучения. При использовании различных методов многообразия обучения, предназначенных для решения различных проблем сокращения размерности, каждый из которых включает в себя несколько параметров для установки, приложение не всегда прямолинейно. В зависимости от ожидаемого базового пространства, необходимо сделать выбор для линейного или нелинейного метода. Нелинейные методы, описанные выше, минимизируют объективную функцию, основанную на локальной окрестности во входном пространстве. Важнейшим параметром с этими методами является k, количество соседей, рассматриваемых для каждого субъекта, и, следовательно, определение ожидаемой степени нелинейности.
Необходимо также сделать еще один важный выбор в отношении меры ввода, независимо от того, основана ли она на метрике расстояния или является чистой мерой подобия. В то время как дистанционная мера может быть преобразована в подобие (например, с использованием теплового ядра), это преобразование приносит с собой дополнительный параметр t. Точно так же мера, основанная на подобии, может быть преобразована в дистанционную меру только при определенных предположениях. Поэтому рекомендуется применять метод внедрения, который легко справляется с доступной мерой ввода. Входная мера, используемая при многообразии в этой работе, основана на сходстве интенсивности. Поскольку данный подход может легко справляться с сходствами, он используется для всех приложений, описанных ниже[9].
В качестве демонстрации представленые результаты, полученные по различным методам внедрения, показаны на рисунке 2. На четырех графиках показаны координаты внедрения многообразия, полученные с использованием MDS, LLE, HLLE и лапласианских собственных карт (LE). Для 167 изображений, полученных из данных субъектов с болезнью Альцгеймера и 231 изображение из данных здоровых людей, парная мера сходства sij определяется как взаимная корреляция между каждой парой изображений xi и xj. Для методов обучения на основе расстояния подобие sij преобразуется в расстояние dij с dij = 1 - sij. Размер окрестности k = 15 используется для всех разреженных методов. Первые два измерения полученных координат вложения нанесены на график для каждого из различных методов (объекты БА изображены синим цветом, а здоровые элементы красным).
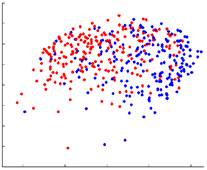
Многомерное масштабирование
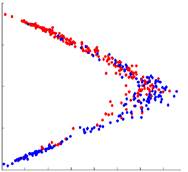
Локально линейное вложение
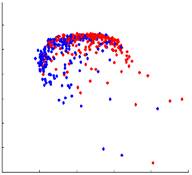
Гессенское локально линейное вложение
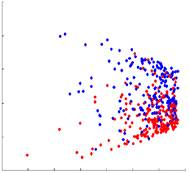
Лапласианские собственные карты
Рисунок 2. 2D-вложения, полученные с различными методами уменьшения размерности до 167 изображений, полученных у пациентов с AD (синий) и 231 изображений по данным здоровых людей (красный).
Заключение. В данной статье описаны методы извлечения признаков или биомаркеров из изображений МРТ. Интересно заметить следующее: не смотря на то, что прогнозы полученные на основе снимков МРТ имеют не лучшее качество, они способны привнести полезную информацию и немного улучшить результат прогноза при использовании их вместе с клиническими признаками. Эффект от представления МРТ виден при долгосрочном прогнозе, а описанные методы позволяют улучшить качество прогноза, особенно при совместном их применении.