1. Введение
Уравнение
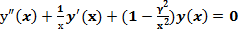(1)
где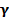 
- порядок функции Бесселя, Фридриха Бесселя немецкого математика ( 1784-1846) впервые определено швейцарским математиком Даниилом Бернулли и назван в честь его . Решение уравнения Бесселя также называют цилиндрическими функциями.Важность исследования решения уравнения Бесселя заключается в том что, оно возникает при решении многих задач математической физики, такие , например, при решении задач Дирихле для клиновидной области , задач теплопроводности в цилиндрических областях, форм колебаний тонкой круглой мембраны, распределений интенсивности света на круглом отверстии, волновых функций в сферически симметричном потенциальном ящике, при обрабоке сигналов и так далее. Поэтому, исследование свойств его решений играют важый роль для прикладной математики.
Обычно, асимптотику решения при больших значения аргумента, т.е. независимой переменной при фиксированной постоянной порядка, получают из его интегральных представления.
Здесь нами предложен альтернативный метод получения его решения, непосредственно из его дифференциального уравнения.
2. Уравнение Бесселя нулевого порядка
Сначала рассмотрим уравнение Бесселя нулевого порядка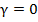 
, т.е.
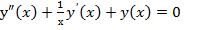(2)
Очевидно, что точка нуль является регулярный особой, а точка на бесконечности иррегулярной точкой этого уравнения. Содержание данной статьи докладывался на международной конференции посвященой восьмидесялетию академика АН УССР А.М. Самойленко [1]
3. Метод сведения к уравнению Риккати
В (2) сделаем подстановку
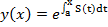, (3)
где a –большое положительное число.
Тогда
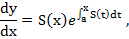
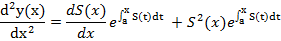
Тогда, подставляя эти выражения для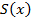 
в уравнение (2), получим уравнение типа Риккати следующего вида
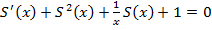(4)
За нулевое приближение решения уравнения (4) берем решение уравнения
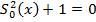
Отсюда
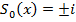
Решение уравнения (4) ищем в виде
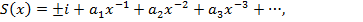(5)
где 
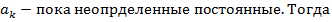
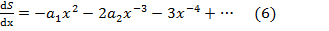
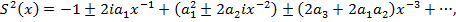(7)
Вставляя (5),(6),(7) в (4) получим
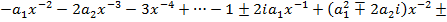
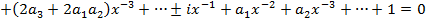
Отсюда приравнивая коэффициентом при одинаковых степенях x, имеем:
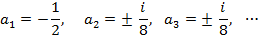
Таким образом
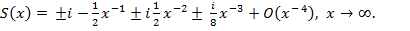
Отсюда, интегрируя это выражение, получаем решение уравнения Бесселя нулевого порядка
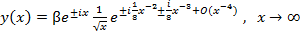
где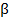 
– некоторая постоянная .Мы получили формальное доказательство следующей теоремы.
Теорема1. Решения уравнения (4) при больших значениях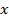 
можно представить следующим асимптотическим рядом
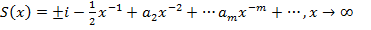(5*)
где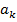 
- некоторые постоянные, т.е. если прервать этот ряд, то он имет вид
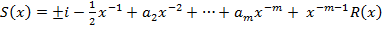
где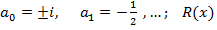 
–ограниченная функция.
Теорема 2. Ряд (5) или (5*) является асимптотическим рядом, то есть
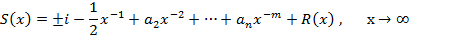
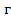де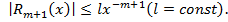
Для простоты эту теорему докажем для m=1, т.е. положим
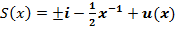(8)
Покажем, что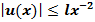 
.
Имеем
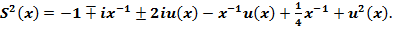(9)
Подставляя (8) и (9) в (4) для u(x) получим следующее уравнение
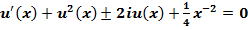(9)
Линейное уравнение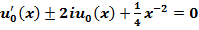 
имеет решение
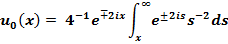
которое стремится к нулю при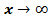
.
Очевидно, это выражение имеет оценку
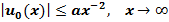(10)
где а-некоторое действительное число.
Обозначим множество функций удовлетворующих условию (10) через Q. Решение уравнения (9) стремящихся к нулю при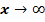 
представим в виде
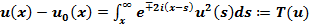(10)
Очевидно, что оператор Т переводит множество Q в себя. Действительно, имеем
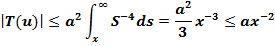
C другой стороны оператор Т является сжимающим в множестве Q. Действительно, дл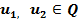я 
имея
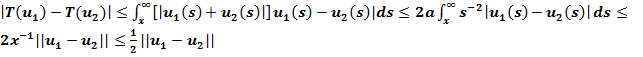
где ||u||=sup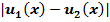 
.
Поэтому для решение уравнения (10) имеет место оценка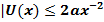 
.
Теорема доказана.
Верна более сильная
Теорема 2. Ряд (5) сходится равномерно при больших значениях x.
Эту теорему докажем методом мажорант. В (10) сделаем преобразование
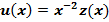(11)
Тогда оно имеет вид
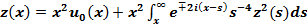(12)
Отсюда, так как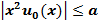 
, отсюда получим следующее мажорантное уравнение для 
:
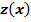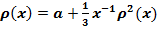
Решение этого уравнения которое ограничено при 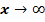имеет вид
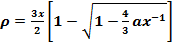(13)
Решение уравнения (13) можно представить в виде сходящегося ряда
+…+
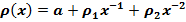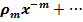
где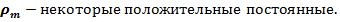 
Таким образом, решение уравнения (6) представляется сходящимся рядом (5) при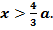 
Далее рассмотрим уравнение Бесселя любого порядка
4. Уравнение Бесселя любого порядка
Рассмотрим уравнение
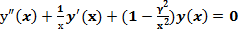, (1)
где 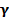- порядок функции Бесселя. После преобразования (2), это уравнение имеет вид
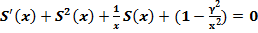(14)
Решение этого уравнения при больших значениях аргумента x , ищем в виде ряда
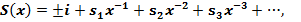(15)
Тогда, подставляя (14) и (15) в уравнение (1) для значений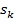 
имеем значения
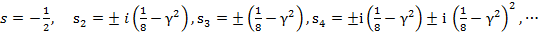. (16)
Таким образом, мы получили формальное доказательство следующей теоремы
Теорема 3 Решение уравнения (14) при больших значения аргумента x можно представить в виде ряда (15),где коэффициенты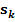 
, из выражений (16).
Полное доказательство этой теоремы можно получить методом мажорант , точно также как и выше.
Замечание1. Разложение при больших значениях аргумента для модифицированного уравнения Бесселя
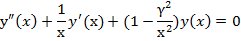
также можно получить этим методом.
Замечание 2. Асимптотику решения уравнения Бесселя при больших значения аргумента, также можно получить, прямо из исходного уравнения (14).
Заключение
Здесь асимптотика решения уравнения Бесселя при больших значения независимой переменной получена непосредственно из самого дифференциального уравнения, причем даказана сходимость полученного решения методом мажорант.