В статьях одного из соавторов обосновывалось применение обобщенных укрупнённых дидактических единиц (ОУДЕ), введённых в [1]. В статье [2] отмечалось, что ОУДЕ охватывают «весь комплекс математических операций, характерных для данной темы или раздела».
В данной статье рассмотрим вопросы теории одномерных множеств, включаемых в интерактивные обучающие документы информационной образовательной среды (ИОС). Указанное представляет собой актуальность проблемы. Практическая новизна проблемы состоит в подготовке учебных материалов «нового типа». Предлагаемые нами ОУДЕ являются продолжением, развитием укрупнённых дидактических единиц (УДЕ) академика Эрдниева П.М. [3].
Рассмотрим сначала задачу УДЕ. Рассматриваемая задача на единственное решение, в аналогичных задачах задавались либо интервалы, либо сегменты, либо полуинтервалы. В домашних работах обучающиеся решают аналогичные задачи.
Прямая задача (Direct problem) № 1.
I.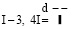 
II.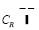 
.
III.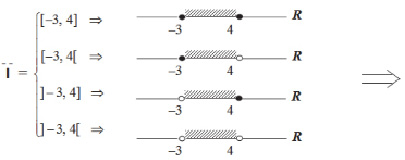 
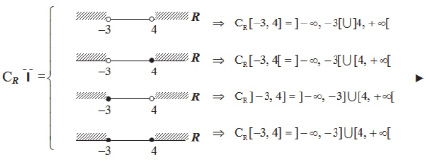
Решение приведено с использованием логико-речевой символики (ЛРС) ([4]). Очевидно, что подобное оформление решения УДЕ намного понятнее словесного. У обучающихся в результате формируются единые символы – формулы и рисунок – как единое целое, возникает так называемый «кибернетический эффект».
Поначалу это замечают только решающие соответствующую задачу, но после выполнения домашнего задания, аналогичного решённому на занятии, указанное становится достоянием (знанием) всех выполнивших задание.
Рассмотрим обратную задачу. То, что нужно было найти в прямой задаче – теперь условие обратной.
Обратная задача (Inverse problem) № 2.
I. CR A = ]–∞, 3I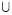
I7, +∞[.
II. A.
III.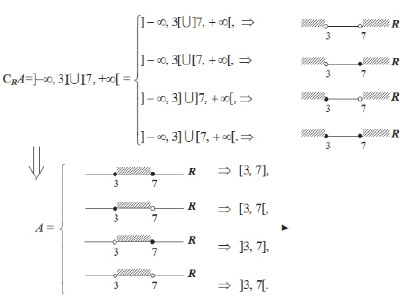 
Рассмотрим следующую задачу (ОУДЕ) на множестве универсума U состоящую в том, что вычисление дополнения будет производиться до некоторого отрезка, или объединения отрезков, включающих в себя заданный отрезок. Количество вариантов решения – количество подмножеств множества концов отрезков в количестве 4, т.е. 24 = 16 (кардинальное число), в зависимости от включения/исключения концов отрезков во множество.
Прямая задача (Direct problem) № 3.
I. A = I0, 4I \ {3} ∧ B = I–1, 5I.
II. CB A.
III. A = I0, 4I \ {3} ∧ B = I–1, 5I :
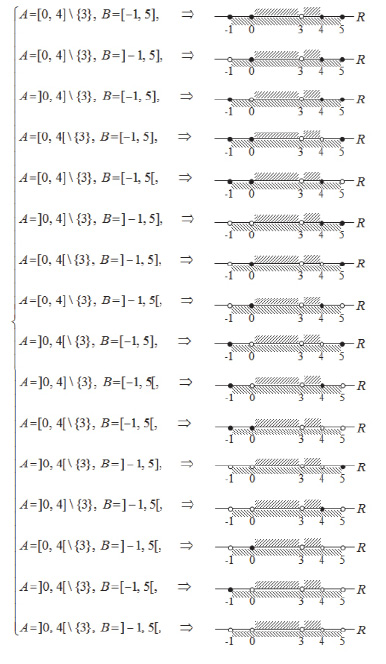
CB A =
Обратная задача решается аналогично. В решении прямой задачи использована логико-речевая символика [4], каждое множество в решении изображено графически, поэтому приведённое решение понятнее формульного без графики, кроме того создаются стойкие логические цепочки во время решения аналогичных вариантов ([5]).
Приведённое решение позволяет ввести данную ОУДЕ в интерактивный обучающий документ и организовать тестирование, которое также будет активным и интерактивным, как и само решение, с множеством вариантов ([6]). Напомним, что ОУДЕ – задача, в которой сосредоточено большое количество математических операций, изучаемых в текущей теме (разделе).
Обучающиеся, решая аналогичную задачу с использованием интерактивной доски (обычная доска с мелом и тряпкой использовать просто нереально) в обязательном порядке вспоминают и применяют все изученные математические операции, выполняя при этом графические построения. По этой причине изучаемый материал ещё на нижнем коде (доречевом) становится знанием обучающихся до перекодировки на словесном уровне.