Наряду с колебательными системами, в которых энергия с течением времени может только уменьшаться из-за диссипации, существуют и такие, в которых возможно пополнение энергии колебаний за счет неустойчивостей. Это может иметь место, когда система в состоянии обмениваться с окружающей средой энергией или веществом, т.е. является энергетически открытой [3].
В открытых системах возникают автоколебания. Это незатухающие колебания в нелинейных диссипативных системах, характеристики которых – амплитуда, частота, форма колебаний определяются параметрами самой системы и не зависят от конкретных начальных условий.
В общих чертах понять природу этого явления – режима автоколебаний можно с помощью качественных соображений.
С течением времени фазовые траектории системы автоколебаний стремятся к некоторому притягивающему множеству – аттрактору. В случае периодических автоколебаний в фазовом пространстве системы наблюдаются устойчивые предельные циклы.
Осциллятор Ван дер Поля: условия устойчивости состояния равновесия. Основной математической моделью при исследовании периодических автоколебательных систем является уравнение осциллятора Ван дер Поля:
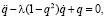(1)
где q – динамическая переменная; ? – постоянная величина, управляющая возбуждением автоколебаний. Рассмотрим случай мягкого самовозбуждения системы, когда после сколь угодно малого начального возмущения состояния равновесия наблюдаются колебания с малыми амплитудами. Пока колебания малы и выполняется неравенство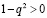 
, второе слагаемое уравнения Ван дер Поля будет оказывать дестабилизирующее действие, и колебания будут возрастать. Но с их увеличением указанное неравенство станет нарушаться и коэффициент при 
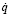будет положительным в тех интервалах времени, в которых 
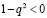. B этих интервалах времени второе слагаемое уравнения будет оказывать демпфирующее влияние. При дальнейшем возрастании колебаний демпфирующее действие будет увеличиваться, и движение системы станет приближаться к стационарному режиму, которому соответствует взаимная компенсация дестабилизирующего и демпфирующего влияний [5]. Движение системы будет стремиться к режиму автоколебаний, которому соответствует постоянное значение амплитуды (рис. 1).
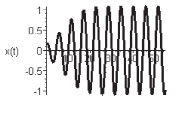
Рис. 1. Автоколебательный режим
При определении условий возникновения автоколебаний важно знать, какие состояния равновесия существуют в системе, и как меняется характер их устойчивости в зависимости от управляющих параметров [3].
Для нахождения точек равновесия и определения характера их устойчивости в осцилляторе Ван дер Поля, обычно рассматривается уравнение (1) в виде
,
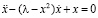или, по-другому, в форме системы обыкновенных дифференциальных уравнений первого порядка:
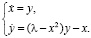
Для нахождения особых точек – положений равновесия решается система уравнений
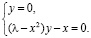
Система имеет только тривиальное решение – единственную точку покоя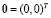 
.
Для определения устойчивости состояния равновесия рассматривают линеаризованную систему в окрестности точки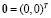 
. Матрицу линеаризации системы вычисляют по формуле
.
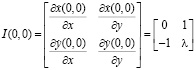Для анализа поведения фазовых траекторий в локальной окрестности состояния равновесия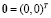 
учитываются собственные значения матрицы линеаризации [3, 4]:
1. Если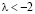 
, тогда собственные значения матрицы – отрицательные действительные числа. Состояние равновесия представляет собой устойчивый узел.
2. Если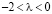 
, тогда собственные значения матрицы – комплексно-сопряженные числа с отрицательной действительной частью. Состояние равновесия – устойчивый фокус.
3. Если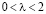 
, тогда собственные значения матрицы – комплексно-сопряженные числа с положительной действительной частью. Состояние равновесия является неустойчивым фокусом.
4. Если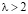 
, тогда собственные значения являются действительными положительными числами. Состояние равновесия представляет собой неустойчивый узел.
Численное моделирование. Описанное поведение фазовых траекторий осциллятора Ван дер Поля относительно состояния равновесия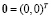 
проиллюстрированы с использованием численного моделирования. На рисунках представлены фазовые портреты и формы колебаний динамических переменных осциллятора.
Для случая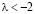 
мы действительно наблюдаем, что начало координат 
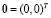является особой точкой типа устойчивый узел (рис. 2).
На рис. 3 при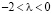 
фазовая траектория представляет собой спираль, скручивающуюся к точке 
– устойчивому фокусу.
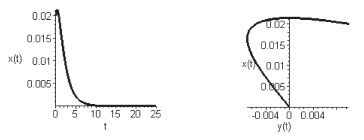
Рис. 2. Форма колебаний и фазовый портрет для осциллятора Ван дер Поля при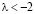 
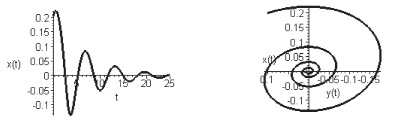
Рис. 3. Форма колебаний и фазовый портрет для осциллятора Ван дер Поля при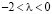 
Если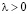 
, то состояние равновесия в начале координат теряет свою устойчивость (рис. 4, 5).
Замкнутые кривые, к которым неограниченно приближаются все фазовые траектории, описывают стационарные режимы автоколебаний и являются устойчивыми предельными циклами. Их областью притяжения служит вся фазовая плоскость.
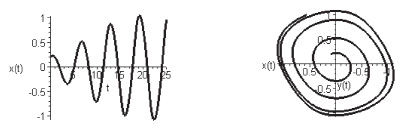
Рис. 4. Форма колебаний и фазовый портрет для осциллятора Ван дер Поля при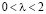 
При малых положительных ? предельный цикл имеет форму близкую к эллипсу. Форма автоколебаний будет близка к гармонической (рис. 4). При увеличении ? предельный цикл меняет свою геометрию, искажается. Форма автоколебаний будет иметь релаксационный вид (рис. 5). При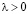 
меняется и характер состояния равновесия 
: неустойчивый фокус переходит в неустойчивый узел.
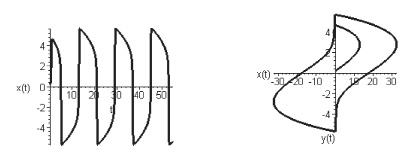
Рис. 5. Форма колебаний и фазовый портрет для осциллятора Ван дер Поля при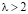 
Заключение
В работе было проведено качественное исследование решений уравнения Ван дер Поля, описывающих переход от состояния неустойчивого равновесия к устойчивому предельному циклу. Генератор Ван дер Поля является достаточно простой и общей моделью периодических автоколебаний. Наиболее частое применение это уравнение находит в радиофизике при построении автогенератора электромагнитных колебаний [3]. Современная теория синтеза структуры нелинейной колебательной системы для получения устойчивых предельных циклов развивается в направлении усложнения геометрии циклов и увеличения их числа (многоканальные системы). Задача создания методов синтеза автоколебательных режимов для многомерных систем остается актуальной [1, 2].