Какие бы изменения не происходили в обществе, они обязательно влекут за собой изменения и в школьном образовании. Меняется структура и содержание, цели и задачи, приоритеты образования и, как следствие, меняются требования, предъявляемые к школьному учителю и ученику.
В течение последних лет школьное образование в нашей стране претерпевает значительные изменения. Осуществляется переход от традиционной системы обучения, направленного на накопление ЗУНов (знаний, умений, навыков), к личностно-ориентированному обучению. Развитие личности школьника – одна из главных задач, которую ставят федеральные государственные образовательные стандарты общего образования нового поколения. Поставленная задача предполагает изменение имеющихся и внедрение новых образовательных технологий. В свою очередь использование образовательных технологий предполагает освоение учителем инновационных компонентов профессиональной деятельности.
Профессиональная инновационная деятельность школьного учителя математики ведет к разработке и внедрению методического инструментария, фиксирующего новые идеи, подходы к решению проблемы математического развития школьников.
Учитывая все сказанное выше считаем, что в условиях реализации ФГОС ООО одной из актуальных образовательных технологий является педагогическая технология В.М. Монахова [1]. На основе этой технологии (ее сущностных характеристик и принципов) по предмету «Математика» (6 класс) нами спроектирован учебный процесс, ориентированный на математическое развитие школьников, и разработан необходимый методический инструментарий: технологические карты учебного процесса по всем темам курса, информационные карты развития учащихся, программы развития, информационные карты уроков [1, 2, 3, 4].
В данной работе в качестве примера представим проект учебного процесса по теме «Отношения и пропорции», ориентированного на математическое развитие учащихся 6 класса.
|
ТЕХНОЛОГИЧЕСКАЯ КАРТА №1 Предмет Математика Ф.И.О. Бессонова В.В. (авторская педагогическая технология В.М. Монахова) класс 6 учителя В.М. Монахов ТЕМА Отношения и пропорции |
||||||||||||||||||||||||||||||||||||||||||||||
|
Логическая структура учебного процесса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
||||||||||||||||||||||
|
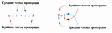
В1 Р/3 Р/3 Д1 В2 Р/3 Д2 В3 Р/3 Р/3 Д3 В4 Д4 В5 Р/З Н/М Р/З Н/М Д5 –––> ––––––––––––––––> мышление память ––––––––––––––––> восприятие |
||||||||||||||||||||||||||||||||||||||||||||||
|
Целеполагание |
Дата |
Диагностика |
Дата |
Коррекция |
||||||||||||||||||||||||||||||||||||||||||
|
B1 Знать, что называют отношением двух чисел. Знать основное свойство отношения, основное свойство пропорции. Уметь устанавливать образуют ли отношения пропорцию. |
Д1 1. Найдите отношение: 3 дм : 5 см 2. Запишите в виде пропорции утверждение: отношение 7,2 к 0,8 равно отношению 0,09 к 0,01. 3. Решите уравнение: 4. Нарушится ли пропорция, если: 1) оба члена одного из отношений умножить на 5; 2) оба члена одного отношения разделить на 4, а оба члена другого отношения умножить на 10; 3) оба средних члена разделить на 3,5. |
К1 Возможные затруднения связаны с определением крайних и средних членов пропорции.
Устранимы при помощи данной схемы и выполнении подобных заданий на основное свойство пропорции. |
||||||||||||||||||||||||||||||||||||||||||||
|
B2 Знать, что называют процентным отношением. Уметь решать задачи, пользуясь правилом нахождения процентного отношения двух чисел. |
Д2 У Кати было 170 марок, 119 марок она подарила Вале. Какой процент всех своих марок она подарила? Цена товара снизалась с 350 рублей до 280 рублей. На сколько процентов снизилась цена? Костюм стоил 1800 руб. Сначала его цену повысили на 20 %, а затем новую цену снизили на 10 %. Какой стала цена костюма после этих изменений? На сколько процентов изменилась начальная цена костюма? На сколько процентов увеличится число при увеличении его в 2,5 раза? |
K2 Возможные ошибки при записи условий текстовых задач, составлении численных и буквенных отношений. Устранимы в ходе решения подобных соответствующих задач. |
||||||||||||||||||||||||||||||||||||||||||||
|
B3 Знать какие величины являются прямо пропорциональными, обратно пропорциональными. Уметь устанавливать являются ли величины пропорциональными. Уметь решать задания на пропорциональность величин. |
Д3 В таблице приведены соответствующие значения величин x и y. Установить, являются ли эти величины пропорциональными.
Две швеи за день сшивают 12 платьев. Сколько им нужно работать, чтобы сшить 36 платьев? 60 платьев? Велосипедист проехал 48 км. Заполните таблицу, в первой строке которой указана скорость велосипедиста, а во второй – время движения. Задайте формулой зависимость t от v.
Бригада из 15 рабочих может отремонтировать школу за 46 дней. Сколько требуется рабочих, чтобы отремонтировать эту школу за 30 дней, если производительности труда всех рабочих одинаковы? |
K3 Возможные ошибки в определении, где прямая, а где обратная пропорциональная зависимость. Устранимо при повторении определений и последующем решении подобных заданий. Затруднения связаны при решении текстовых задач, в записи условий. Устраняется в результате решения типовых задач. |
||||||||||||||||||||||||||||||||||||||||||||
|
В4 Уметь делить число в данном отношении. |
Д4 Разделите число 140 в отношении 3:6:8:11. Периметр треугольника равен 48 см, а длины его сторон относятся как 7:9:8. Найти стороны треугольника. Начертите развернутый угол АВС и проведите луч BD, чтобы градусные меры углов ABD и CBD относились как 15:21. Представьте число 219 в виде суммы трёх слагаемых x,y,z так, чтобы x:y=4:9, а y:z=15:2 |
К4 Возможны ошибки Разделить число 520 в данном отношении 8:5. Ошибки: 520:8=65 65•5= 325. Устраняется при отработке алгоритма деления числа в данном отношении. |
||||||||||||||||||||||||||||||||||||||||||||
|
В5 Уметь распознавать геометрические фигуры: окружность, круг, цилиндр, конус, шар. Знать формулы длины окружности, площади круга, площади боковой поверхности цилиндра. Уметь вычислять по этим формулам. |
Д5 Вычислить длину окружности, диаметр которой равен 4,2 см. Радиус основания цилиндра равен 4 см, а его образующая – 9 см. Найдите площадь боковой поверхности цилиндра. Найдите площадь круга, если Квадрат, площадь которого равна 81 см2, вращают вокруг одной из его сторон. Вычислите площадь боковой поверхности образовавшегося цилиндра. |
К5 Возможны ошибки при использовании формул на нахождение длины окружности, площади круга, площади боковой поверхности цилиндра. Возможная путаница между радиусом и диаметром. Устранимо повторением формул, решением задач с их использованием. |
||||||||||||||||||||||||||||||||||||||||||||
|
Дозирование самостоятельной деятельности учащихся |
||||||||||||||||||||||||||||||||||||||||||||||
|
СТАНДАРТ |
ХОРОШО |
ОТЛИЧНО |
||||||||||||||||||||||||||||||||||||||||||||
|
Б1 № 581,584,605 Б2 № 635, 639 Б3 № 663, 665(4), 667 Б4 № 683 Б5 № 704, 706, 734,770,773 |
Б1 № 593, 618 Б2 № 648 Б3 № 673 Б4 № 687 Б5 №741, 775 |
Б1 № 624 Б2 № 650 Б3 № 675 Б4 № 693 Б5 № 761, 776 |
||||||||||||||||||||||||||||||||||||||||||||
Комментарий к технологической карте.
В логической структуре учебного процесса включены следующие специальные программы развития: мышление, восприятие, память.
Для решения планируемых задач развития и получения положительных результатов в программах развития определены специальные упражнения.
Специальная программа развития «Мышление» на уроках математики в 6 классе при изучении темы «Отношения и пропорции»
Пояснительная записка
Мышлением называют высший познавательный и регулятивный процесс. От прочих психологических процессов познания мышление отличает его постоянная связь с активным изменением условий, в которых пребывает человек. Мышление всегда нацелено на решение какой бы то ни было задачи. В процессе мышления происходит преобразование действительности.
В курсе 6 класса много текстовых задач, при решении которых развивается мышление.
Мы рассмотрим в частности практическое мышление. Его особенность заключается в тонкой наблюдательности, концентрации внимания на отдельны составляющих, использование при решении частной задачи того, что не входит целиком в теоретическое обобщение, быстрый переход непосредственно к действию от размышлений.
В ходе проектирования учебного процесса в теме «Отношения и пропорции» стоит учитывать, что особая цель в научении детей – решать задачи. В процессе решения задачи происходит «обращение» ко многим мыслительным операциям.
Тема «Отношения и пропорции» (уроки № 6,7)
Задачи на развитие практического мышления.
1. Коллекция нумизмата состоит из 2000 монет. Из них 21 % старинных монет, 2 % иностранных, 10 % юбилейных. Сколько монет каждого вида в коллекции?
2. На опытном поле площадь которого 20000 <<bs6.wmf>> растут разные сельскохозяйственные культуры. 30 % площади занято капустой, 23 % морковью, 24 % луком. Какую площадь занимает каждая из этих культур?
3. Мария прочитала книгу за 3 дня. В первый день она прочитала 50 страниц, что составило 20 % от книги, во второй день – 15 %, а оставшуюся часть в третий день. Сколько всего страниц в книге? По сколько она прочитала во второй и третий дни?
4. Мясо теряет при варке около 35 % своего веса. Сколько свежего мяса надо взять, чтобы получить 1 кг вареного? Сколько вареного мяса получится из 2 кг свежего?
5. Во время ремонта кухни за замену линолеума было заплачено 1260 рублей, всего на ремонт потратили 6300 рублей. Какой процент от общей стоимости было потрачено на линолеум?
Также можно предложить задания, представленные в учебнике «Математика 6 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир – М.: Вентана-Граф, 2015.: №640, 646, 647, 649,652.
Специальная программа развития «Память» на уроках математики в 6 классе при изучении темы «Отношения и пропорции»
Пояснительная записка
Память – это умение воспроизводить прошлый опыт, свойство нервной системы, являющееся основным, которое выражается в способности к продолжительному хранению информации и неоднократному введению ее сферу сознания и поведения. Основными процессами являются запоминание, сохранение, воспроизведение. Так же память делят на произвольную и непроизвольную, непосредственную и опосредствованную, кратковременную и долговременную.
В рамках данной программы развития рассмотрена долговременная память.
Целью программы является планирование работы учителя по развитию навыков учащихся в решении задач на нахождение длины окружности, площади круга, площади боковой поверхности цилиндра, и как следствие запоминания формул для нахождения данных величин.
Система заданий предполагает оттачивание умений применять формулы.
Тема «Отношения и пропорции» (уроки № 14–18)
Задания на развитие памяти
1. Определите радиус круга, площадь которого равна:
а) 12,56 м2; б) 1,1304 см2; в) 2,5434 м2; г) 153,86 см2.
2. Изобразите круг, проведите диаметр, радиус и укажите их длины, если площадь круга равна:
а) 28,26 см2; б) 113,04 см2; в) 0,5024 м2.
3. Выполните необходимые измерения и найдите площадь фигуры

4. Считая π равным 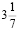 , вычислите, какое расстояние пройдет колесо, диаметр которого 1
, вычислите, какое расстояние пройдет колесо, диаметр которого 1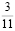 м, если оно совершит три оборота?
м, если оно совершит три оборота?
5. Диаметр основания цилиндра равен 12 см, а его образующая 23 см. Чему равна площадь боковой поверхности цилиндра?
6. Радиус шара равен 27 см. Вычислите площадь сечения шара плоскостью, проходящей через центр шара.
Также можно предложить задания, представленные в учебнике «Математика 6 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир – М.: Вентана-Граф, 2015.: № 744,746,750,755,769,772
Специальная программа развития «Восприятие» на уроках математики в 6 классе при изучении темы «Отношения и пропорции»
Пояснительная записка
Восприятие определяют в качестве сложного процесса приема и преобразования получаемой извне информации. При данном процессе обеспечивается отражение объективности реального мира и ориентация в нем.
Говоря о развитии восприятия как таковом, можно сказать, что оно обуславливается увеличением опыта, знаний, усилением его связей с мышлением, памятью, вниманием, воображением.
Восприятие, будучи формой отражения действительности, позволяет определить объект как целое, обусловить отдельные признаки предмета, отличающие его, выделить в нем качественные детали.
Говоря о математике 6 класса, можно отметить геометрическую составляющую курса. Это так называемый пропедевтический курс. Восприятие в нем играет не малую роль, так как знакомство с геометрическими фигурами и телами позволяет дать фундамент для дальнейшего изучения.
Целью данной программы развития является формирование устойчивого результата в распознавании предмета, выделении его признаков.
Тема «Отношения и пропорции» (уроки № 15–19)
Задания, для распознания геометрических фигур, их сравнение между собой.
1. Назовите предметы, какой геометрической фигуре они соответствуют?

2. Назовите каким геометрическим телам соответствуют данные предметы?

3. Приведите свои примеры предметов, имеющих цилиндрическую форму, форму конуса, шара.
4. Начертите окружность, круг, шар. Сравните их между собой.
5. Из предметов какой формы сложена башня?
6. На рисунке найдите цилиндр, конус, шар.
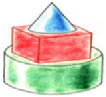
7. Сравните, чем схожи цилиндр, конус, шар.
Можно предложить задачи, представленные в учебнике «Математика 6 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир – М.: Вентана-Граф, 2015.: № 699,700,724,739, 741,767, 768.


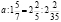
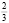
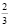 длины окружности этого круга равны 24,8 см (число p округлите до десятых).
длины окружности этого круга равны 24,8 см (число p округлите до десятых).