Сложная система – система, для которой характеристики отношений местоположений по элементам (или группам элементов) играют большую роль, если рассматривать функционирование систем, то есть, и с точки зрения проведения анализа и синтеза систем.
В сложных системах характерным является то, что функции, ресурсы распределяются между совокупностью элементов (узлов) и отсутствует единый управляющий центр, в этой связи, если выйдет из строя один из узлов, то при этом не будет полная остановка всей системы.
На основе вышесказанного можно обосновать актуальность данной работы, цель которой заключается в построении эффективной модели распределения электрических ресурсов, разработке и реализации алгоритма расчета параметров рассматриваемой сложной системы.
В соответствии с целью выделим основные задачи:
• cформулировать задачу распределения электрических ресурсов в системе;
• построить математическую модель задачи;
• обосновать выбор математического метода решения задачи;
• разработать алгоритм расчета параметров распределенной системы электропитания;
• реализовать алгоритм в системе математических вычислений MATLAB;
• проанализировать полученные результаты расчетов и выполнить прогноз параметров сложной электрической системы.
Задачи, связанные с распределением ресурсов относят к оптимизационному типу и их можно рассматривать как в односетевых, так и в многосетевых комплексах работ [1–3]. Исходя из результатов решения задач распределения ресурсов, проводят составление календарного плана исполнения комплекса работ, то есть по каждой работе идет указание дат ее начала и окончания при учете обусловленных технологиями последовательностей их выполнения так, чтобы были удовлетворены оптимальные значения целевой функции и не было нарушение ограничений, которые задаются, когда ставится задача распределения ресурсов [4]. Существует весьма большое количество разных постановок подобных задач, их есть возможность распределить по трем основным группам, в зависимости от того, какой принимается критерий оптимальности и вид ограничений:
– задачи, связанные с распределением ресурсов, при котором достигается минимизация времени по осуществлению комплекса работ при этом выполняются заданные ограничения для используемых ресурсов;
– задачи, связанные с распределением ресурсов, при котором происходит удовлетворение наилучшего значение определенного показателя по качеству применения ресурсов для заданных сроков исполнения всего комплекса, во многих случаях в такой постановке идет минимизация максимальных значений по потребляемым ресурсам;
– задачи, связанные с распределением ресурсов в смешанных постановках, где, например, для определенных сетях в многосетевых разработках идет минимизация времени исполнения комплекса работ для заданных уровней применяемых ресурсов, а для других – идет минимизация уровней потребления ресурсов для заданных сроках исполнения комплекса.
Способы решения задач по распределению ресурсов [5] можно условным образом разделить по: 1. методам математического программирования; 2. эвристическим; 3. комбинированным.
Методы в первом направлении реализуют на основе средств целочисленного динамического, статистического, линейного, нелинейного, программирования. Во втором направлении рассматривают методы, которые базируются на эвристических правилах (методе последовательного фронтального распределения, методе последовательного растяжения, методе последовательной корректировки плана и др.).
Для комбинированных методов решения задач по распределению ресурсов в качестве основы рассматривают сочетание методов математического программирования и эвристических методов и их можно условным образом разделить на четыре группы:
1. методы, которые используют результаты решения задачи на основе эвристических методов в качестве исходных данных с тем, чтобы в дальнейшем осуществлять решение на основе методов математического программирования;
2. методы, в рамках которых происходит предварительное эвристическое деление основных задач на частные задачи, которые решаются на базе методов математического программирования;
3. методы, применяющие эвристические правила, когда формируются условия задачи, которая решается методами математического программирования;
4. усеченные методы математического программирования.
Методы, связанные с распределением ресурсов есть возможность разбить на методы, при переменной и постоянной интенсивности использования ресурсов, применяемых на работах. Методы, связанные с распределением ресурсов при переменной интенсивности потребления ресурсов основываются на возможности изменения интенсивностей потребления ресурсов во время исполнения любых работ, что ведет в конечном итоге к тому, что сокращается продолжительность исполнения работ и увеличивается коэффициент использования ресурсов. В результате того, что решаются данные задачи, можно получить зависимость оптимальных значений потребляемых ресурсов от длительности каждой работы сетевой модели [6, 7].
В случаях, когда рассматриваются небольшие сетевые модели задачи распределения ресурсов при переменной интенсивности можно решать на основе того, что проводится интуитивное перераспределение ресурсов. Когда используются графики больших размерностей требуется привлекать методы математического программирования.
Методы, связанные с распределением ресурсов при условии постоянной интенсивности потребления ресурсов, применяемых на работах, есть возможность разбить по двум большим группам:
– методы, рассматривающие фиксированную интенсивность потребления ресурсов;
– методы, рассматривающие фиксированный диапазон по возможным значениям интенсивностей потребления ресурсов.
Когда используются методы, относящиеся к первой группе, то заранее идет задание интенсивности потребления ресурсов и проводится поиск по оптимальным срокам начала и окончания работ. В качестве недостатка таких алгоритмов можно отметить то, что качество решения, которое определяется, прежде всего, на основе коэффициента использования ресурсов, большей частью зависит от того, какие интенсивности потребления ресурсов, которые назначают, базируясь на опыте и инструкции.
Когда используются методы, относящиеся ко второй группе, производится поиск по оптимальным интенсивностям потребления ресурсов во внутренней области заданных диапазонов, а также по срокам старта и окончания работы. Размерности подобных задач, которые решаются на основе классических методов математического программирования при реальных сетевых моделях, будут неприемлемы для современных объектов вычислительной техники.
Одним из условий того, что применим метод динамического программирования являют возможности разбиения процессов оптимизации решения на совокупность однотипных шагов (этапов), для каждого из которых идет планирование отдельным образом, но при учете состояния системы по началу этапа и последствиям принятых решений [8, 9]. Следует отметить, что после последнего шага, больше нет этапов. Его можно изучить и спланировать наилучшим образом. В результате получается одна из особенностей в динамическом программировании: вычислительная процедура программирования должна быть развернута от конца к началу. Ранее всех идет планирование последнего N-го шага, за ним (N–1)-го и т. д. Каким образом может быть найдено оптимальное управление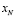 
для N-го шага, если оно основывается не только на том, какая цель управления, но и какое состояние системы на начало такого шага? Это может быть сделано исходя из предположений о том, какие ожидаемые исходы по предшествующему, но еще не исследованному этапу, то есть о значениях 
.
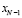В структуре целевой функции отражается вклад по каждому типу производственной деятельности в общие результаты. Когда рассматривается случай максимизации, то cj, является прибылью от j-го типа производственной деятельности на единицу соответствующей продукции, а если рассматривается случай минимизации, то сj связано с удельными затратами. Отметим, что нельзя сделать вывод о «полезности» определенных типов производственной деятельности лишь на основе значений соответствующих коэффициентов целевой функции, поскольку объем получения ограниченных ресурсов также может рассматриваться как важный фактор [10–12]. Так как все типы производственной деятельности, которые представляются в модели, рассматривают возможность использования ограниченных ресурсов, относительная полезность по некоторому типу производства (если сравнивать с другими типами производственной деятельности) определяется как величиной коэффициента целевой функции cj, так и интенсивностью получения ресурсов aij. В этой связи может получиться, что вследствие того, что слишком большой расход ограниченных ресурсов, некоторый i-й тип производственной деятельности, который характеризуется высокой прибылью, применять нецелесообразно (то есть для оптимального решения xj=0).
Под варьируемой (оптимизируемой) величиной будем понимать некоторую величину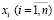 
которая будет обозначать электрическую мощность V, которую надо передать в i-й район.
Тогда целевая функция запишется в следующем виде:
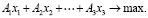(1)
Т.е. объём потребления электрической мощности стремиться к своему максимальному значению.
Введем два ограничения для целевой функции. Одно – ограничение для ресурса R. Второе ограничение будет на значение тока в электрической цепи. Таким образом, ограничения, накладываемые на целевую функцию, будут иметь вид:
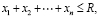(2)
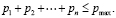(3)
Для удобства изменим условия задачи. В данном случае постановка задачи следующая: «какую мощность надо передать, чтобы получить нужное значение тока». Рассмотрим обратную задачу: «какой нужно создать ток, чтобы передать необходимую мощность». Последняя формулировка задачи более применима на практике, чем первая.
С учетом новых условий задачи изменим варьируемые параметры. В последнем случае изменяемым параметром будет непосредственно ток p, а не мощность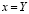 
, как предполагалось ранее. Для этого с помощью физических преобразований мощность выражается через ток.
После подстановки полученного соотношения в целевую функцию и ограничения, получаем математическую модель задачи, в которой основным изменяемым параметром будет электрический ток.
Для решения задач линейного программирования (4) – (6), представляющих собой математические модели распределительной системы электропитания с различными параметрами, разработаны математические методы решения, такие как симплекс-метод, графический метод решения задач линейного программирования, модификация симплексного метода – метод искусственного базиса.
При построении математической модели важным фактором является выбор алгоритма решения поставленной задачи.
В настоящее время существует множество численных алгоритмов решения задач. Каждый из них характеризуется своими преимуществами и своими недостатками. К преимуществам можно отнести небольшое количество выполняемых итераций необходимых для поиска оптимального решения, выполнение линейных операций, так как это требует гораздо меньших затрат ресурсов, и основного из них – времени, будь это человек – решающий задачу оптимизации, либо ЭВМ выполняющая аналогичную работу.
Рассмотрим задачу оптимизации в общем виде. Пусть задана целевая функция:
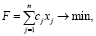
с соответствующим набором ограничений:
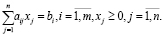
Теперь рассмотрим особенности решения задач подобного класса.
Одним из основных методов, который применяется для решения подобных задач, является симплексный метод с множеством его вариантов.
Классический симплексный метод решения задач линейной оптимизации базируется на том, что происходит переход от одних опорных планов к другим. Такой переход может быть, если мы знаем некоторый исходный опорный план, который составляется из коэффициентов входящих в целевую функцию и в систему ограничений.
Классический симплексный метод включает в себя следующие шаги:
1. Определение начального опорного плана.
2. Составление симплекс-таблицы.
3. Вычисление оценок.
4. Анализ оценок.
5. Определение ведущей строки. Для этого находится отношение правых частей ограничений к положительным элементам ведущего столбца и среди них выбирается минимальное.
6. Осуществляется пересчёт симплекс-таблицы.
7. Переход к шагу №3.
В данной работе рассмотрена задача распределения электрических ресурсов в системе. Составлена математическая модель задачи в виде задачи линейного программирования. Проведены серии тестов при изменении параметров для трех задач.
1. Приоритеты на получение объектами ресурса различны.
2. Приоритеты на получение ресурса равны между собой.
3. Значения в ограничениях при одной переменной превышают все остальные.
Приведены результаты выполнения серий тестов в табличном и графическом представлении. Расчетов оптимальных планов в соответствии с выбранным симплекс-методом решения задач линейного программирования выполнены с помощью математический пакета MATLAB. Выбор данного программного продукта обусловлен наличием встроенной функцию linprog(), реализующий решение симплекс-методом с возможностью просмотра промежуточных результатов, а также наличием в данном пакете широкого спектра средств для графического представления результатов.
Разработан алгоритм расчета параметров распределенной системы. Новизна данной выпускной квалификационной работы заключается в исследовании вопроса прогнозирования изменения параметров системы.
В качестве инструмента прогнозирования применяется аппроксимация реальных значений параметров восьми вариантов тестов (базовые значения) в каждой серии тестов, в качестве средства проверки оптимальности выбора способа аппроксимации, рассчитаны относительные ошибки прогноза (для девятого, десятого и одиннадцатого вариантов тестов – проверочные значения).