В задачах, связанных с расчетом характеристик рассеяния в радиолокационных системах возникают проблемы, связанные с анализом электромагнитных полей [1–3], которые отражаются от объектов, имеющих сложную геометрическую форму и электрофизическую структуру. В течение последнего времени наблюдается накопление большого опыта, связанного с решением подобных задач [5, 6].
Проведение математического моделирования характеристик рассеяния объектов может базироваться на применении метода физической теории дифракции, интегральных уравнений, полигональных моделей.
В состав большого числа технических объектов входят клинья, кромки и другие подобные элементы, имеющие разную форму [7–9]. Представляет интерес с точки зрения практики провести анализ влияния формы поверхности в области центра рассеяния, а также дать рекомендации по обеспечению требуемого уровня характеристик рассеяния.
В данной работе мы рассматривали двумерный подход. Задачу, связанную с дифракцией электромагнитных волн на объектах, мы решали на основе использования двумерного интегрального уравнения Фредгольма первого рода.
Для уравнения Фредгольма первого рода, в которое входит плотность искомого электрического тока для случая Е-поляризации [10] записывается следующее выражение:
, 
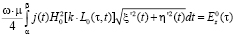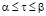, (1)
где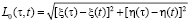 
является расстоянием от точки наблюдения до точки интегрирования, 
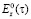– является продольной составляющей напряженности по первичному электрическому полю для точки на контуре. Идет задание контура на основе параметрического представления: 
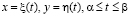, а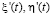 
– являются первыми производными для соответствующих функций, 
, 
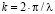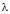– является длиной падающей электромагнитной волны.
Когда мы решали уравнение (1), то был использован метод моментов, в результате интегральное уравнение сводится к системе линейных алгебраических уравнений, после решения, которой определяем продольные электрические токи, имеющие плотность
, 
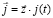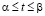, (2)
Для определения двумерной эффективной площади рассеяния (ЭПР) объекта используем следующее выражение
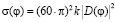, (3)
где
,
.
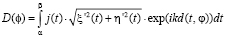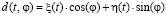На рис. 1, 2, 3 приведены исследуемые объекты.
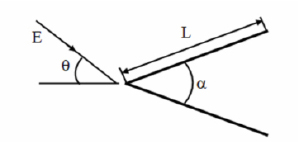
Рис. 1. Схема рассеяния электромагнитной волны на клине
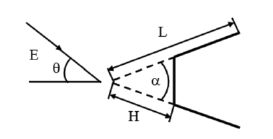
Рис. 2. Схема рассеяния электромагнитной волны на усеченном клине
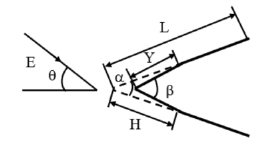
Рис. 3. Схема рассеяния электромагнитной волны на сложном клине
При исследованиях длина ребра клина варьировалась в пределах 3λ≤L≤7λ, угол между боковыми гранями 20°≤α≤40°, длина усеченной части 1λ≤H≤2λ, угол между боковыми стенками при вершине 35°≤β≤55°, сектор углов наблюдения 0°≤θ≤40°.
При расчетах было установлено, что средняя ЭПР объекта, приведенного на рис. 2, превышает среднюю ЭПР объектов, приведенных на рис. 1, рис. 3, более, чем на 3 дБ.
Для того, чтобы решить задачу, связанную с обеспечением требуемого уровня характеристик рассеяния дифракционной структуры, приведенной на рис. 3, для определенного сектора углов наблюдения мы применяли генетический алгоритм (ГА).
Основной особенностью генетических алгоритмов можно считать то, что проводится анализ не одного решения, а некоторого подмножества квазиопытных решений, которые называют хромосомами или стрингами.
В рассматриваемом нами случае хромосома имела 4 гена: b, n, q и w. Так как ген является целым число, которое будет меньше чем 30, то для того, чтобы произвести кодирование по каждому гену мы можем использовать 5 битов. В таком случае хромосома будет представлена в виде, который приведен на рис. 3.
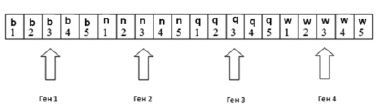
Рис. 4. Схема хромосомы
Для того чтобы произвести поиск решения, была использована популяция из 5 хромосом. Вначале осуществлялся процесс генерации 5 случайных возможных вариантов решений:
F(q,x,c,d), q,x,с,d ∈ {1, 2, 3…30}, (4)
и рассматривалась связь по каждому варианту и ошибке в решении:
δ = | F(q,x,c,d) – FD(q,x,c,d) |. (5)
В качестве примера ниже представлена табл. 1.
Таблица 1
Варианты решения
|
Номер хромосомы |
Вариант (x1, x2, x3, x4) |
Ошибка δ |
Относительная пригодность |
|
1 |
(1, 28, 14,3) |
79 |
0.014 |
|
2 |
(13,8,1,3) |
21 |
0.041 |
|
3 |
(11,4,7,2) |
27 |
0.038 |
|
4 |
(21,8,16,18) |
127 |
0.0068 |
|
5 |
(4,12,29,1) |
24 |
0.036 |
Основная идея работы ГА заключается в том, чтобы был процесс выживания хромосом, которые приводят к меньшей ошибке в решении. Исходя из этого относительная пригодность (ОП) хромосомы описывалась на базе формулы ОП=1/δ.
Для того, чтобы провести вычисление вероятности отбора хромосомы по будущей популяции, мы использовали формулу
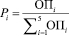, (6)
Результаты использования этой формулы показаны в табл. 2.
Таблица 2
Данные по вероятности отбора хромосом
|
Номер i |
Pi |
Ui, % |
|
1 |
0.014/0.1358=0.1 |
10 |
|
2 |
0.041/0.1358=0.3 |
30 |
|
3 |
0.038/0.1358=0.28 |
28 |
|
4 |
0.0068/0.1359=0.05 |
5 |
|
5 |
0.036/0.1358=0.27 |
27 |
Для того, чтобы осуществить последующие процессы выбора хромосом мы воспользовались методом колеса рулетки. При таком подходе каждая из хромосом имеет соответствующий сектор на колесе Ui (рис. 5).
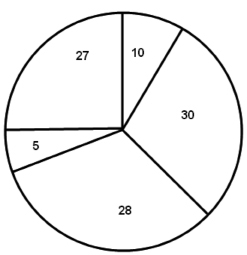
Рис. 5. Демонстрация распределения секторов рулетки
После каждого из вращений колеса, осуществляется процесс выбора определенного сектора, то есть хромосомы. После осуществления 15 вращений колеса, проводится отбор 15 хромосом, среди них исходя из случайного закона идет формирование 5 пар с тем, чтобы происходил процесс скрещивания. Результаты расчетов даны в таблице 3. В качестве примера ниже представлена табл. 3.
Таблица 3
Демонстрация результатов отбора на основе метода рулетки
|
Номер отца i |
Номер матери i |
|
1 |
2 |
|
3 |
2 |
|
5 |
3 |
|
2 |
3 |
|
3 |
5 |
В соответствии с табл. 2 самая плохая хромосома 4 не была отобрана для скрещивания. Хромосому 1 была выбрана для скрещивания только один раз, а хромосомы 2, 3 и 5 были отобраны часто, поскольку для них соответствует высокое значение OП.
Дальнейшей генетической операцией было скрещивание. Средней ошибкой решения для популяции потомков является 58, Но для первоначальной популяции значение этого коэффициента было 67.
В качестве целевой функции мы рассматривали значение средней ЭПР, в заданном секторе углов наблюдения, зависящее от размеров структуры. Для структуры, приведенной на рис. 3, максимальное значение средней ЭПР для сектора углов наблюдения 0°≤θ≤25°, при L=4λ, значении угла между боковыми гранями a=30° было получено для угла между боковыми стенками при вершине β=47°.
В работе проведен анализ характеристик рассеяния электромагнитных волн на клиновидных структурах. Расчет характеристик рассеяния проводился на основе метода интегральных уравнений, проведен сравнительный анализ средних характеристик рассеяния. Рассмотрена возможность оптимизации средних характеристик клиновидных структур на основе генетического алгоритма.