Моделирование процессов рассеяния электромагнитных волн на разных объектах со сложной формой представляет большой практический интерес, вследствие того, что требуется решать задачи, относящиеся к радиолокационному распознаванию, электромагнитной совместимости и др. [1–3].
В ряде случаев, если рассматриваются объекты, имеющие простую форму, достаточно применять аналитические формулы, позволяющие давать довольно неплохие оценки значений характеристик рассеяния [4–6]. При использовании дифракционного подхода объект рассматривается как тело сложной формы, на котором происходит рассеяние радиоволн. Метод интегральных уравнений при рассмотрении его практического применения, является довольно громоздким методом, часто требующим больших ресурсов, как и другие численные методы. Однако если рассматривать структуры, которые являются телами вращения, то наиболее удачным является сочетание методов интегральных уравнений и собственных функций. Главную роль при этом играет угловая, или азимутальная координата j. По этой координате искомые поля, как и при использовании метода собственных функций, разлагаются в ряды Фурье, и поля отдельных гармоник в силу ортогональности оказываются независимыми. Это позволяет для каждой азимутальной гармоники построить сравнительно простое интегральное уравнение, которое решается численно. При этом уменьшается размерность решаемой электродинамической задачи и уменьшаются требования к величине машинной памяти и времени счета ЭВМ.
Существует ряд задач, которые требуют данные не только о том, какие угловые зависимости характеристик рассеяния, но и о том, какие могут быть достигнуты средние их значения, особенно максимальные, для определенных секторов углов наблюдения [7, 8].
Представляет практический интерес построить достаточно простой алгоритм расчета размеров объектов с максимальными средними значениями характеристик рассеяния в определенном секторе углов наблюдения. Для тел простой формы зависимость максимальных средних значений характеристик от размеров тел может быть записана аналитически [9]. В данной работе решена задача определения максимальных средних значений характеристик рассеяния для двумерной модели полой структуры. Аналитическую зависимость максимальных средних значений характеристик рассеяния от размеров объекта в данном случае не удается получить, однако существует возможность построения приближенной функции (интерполирующего полинома), позволяющую получить аппроксимацию этой зависимости при достаточно малой ошибке [6, 7].
В данной работе мы рассматриваем модель расчета размеров двумерного цилиндра, в котором боковая стенка имеет сложную форму, позволяющую определять в заданном секторе углов наблюдения размеры цилиндра с максимальными средними значениями характеристик рассеяния. Применяется следующая модель расчета. На цилиндре мы в качестве характерного размера выделяем размер какого-то его элемента и строим зависимость общей длины контура цилиндра от размера этого элемента.
Характерно то, что применяемый нами способ удобно использовать для цилиндра, имеющего симметрию. Цилиндры входят в состав многих современных объектов техники, при учете мощности вторичного излучения таких структур можно управлять мощностью вторичного излучения всего объекта, причем ее значения могут быть изменены в разы и даже десятки раз. В работе рассматривается двумерная модель. Двумерные модели цилиндров оказываются полезными при проведении оценок характеристик рассеяния трехмерных прямоугольных металлических цилиндров [8].
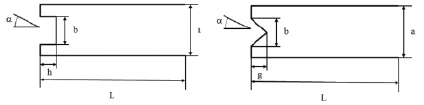
Мы будем считать, что поперечный размер цилиндра равен a, длина L (рис. 1). Боковая стенка цилиндра имеет форму, которая изображена на рис. 1, то есть существует угол наклона β. Тогда общая величина контура цилиндра D=a/(2cosβ)+2L. Нашей задачей будет поиск a и D, при которых значения средней эффективной площади рассеяния (ЭПР) в заданных секторах углов падения электромагнитной волны a дают максимальные значения. Отсчет угла a происходит от направления, параллельного двум стенкам цилиндра.
а б
в
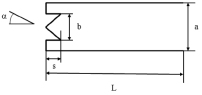
Рис. 1. Иллюстрация рассеяния электромагнитных волн на двумерном цилиндре, имеющем боковую стенку сложной формы (наклон под угломj)
Когда мы проводили анализ характеристик рассеяния, то значения сектора углов наблюдения изменялись довольно значительным образом (от: 5° до 70°), то есть углы относились к области передней полусферы. Значения характеристик рассеяния были получены, основываясь на методе интегральных уравнений [10].
Уравнение Фредгольма первого рода, которое содержит плотность неизвестного электрического тока для случая Е-поляризации [10], записывается, например, следующим образом:
, 
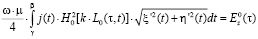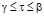; (1)
здесь
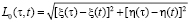
является расстоянием, которое будет между точками наблюдения и интегрирования;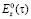 
является продольной составляющей напряженности электрического поля в точке, которая располагается на контуре. Мы задаем контур на основе параметрического представления:
,
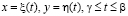а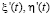 
являются первыми производными по соответствующим функциям, 
, 
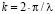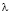– является длиной падающей электромагнитной волны.
При решении уравнения (1) в рамках метода моментов происходит определение продольных электрических токов, имеющих плотность
, 
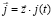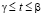, (2)
Расчет двумерной ЭПР металлического цилиндра происходит на основе такого выражения
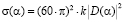, (3)
где
,
.
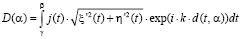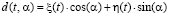Расчет средней ЭПР осуществляется, базируясь на таком выражении
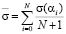, (4)
где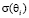 
– равно значению ЭПР при угле наблюдения 
.
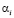Задача определения a и D, которые дают максимальные значения средней ЭПР при определенных секторах углов наблюдения, нами решалась таким образом. Задаем величину сектора углов наблюдения Δα. При различных значениях D происходит определение значений поперечного размера a. Анализ показывает, что функция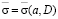 
будет многоэкстремальной, поэтому, когда проводились расчеты, был использован метод сеток [9] при последовательном сужении областей определяемых значений. Для каждого из участков сетки был использован муравьиный алгоритм.
На рис. 2 даны рассчитанные зависимости длины контура D от поперечных размеров цилиндра a, которые позволяют достичь максимальной средней ЭПР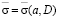 
.
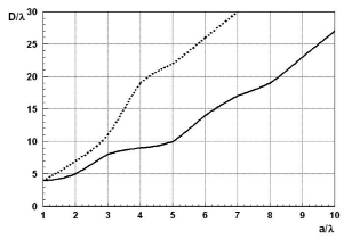
Рис. 2. Зависимость длины контура цилиндра (рис. 1) D от поперечного сечения a для максимальных значений средней ЭПР по сектору углов Δα =7° (кривая 1), Δα =18° (кривая 2) с углом наклона боковой стенки цилиндра β=24º.
Объект сложной формы можно представить в виде совокупности отдельных компонентов (цилиндров, полых структур и т.д.). Для определения характеристик компонентов воспользуемся коэффициентами корреляции. В качестве входных параметров выделим следующие:
1. вид компонента;
2. сектор углов наблюдения;
3. требуемый уровень для средних характеристик рассеяния.
Процесс функционирования подсистемы САПР расчета компонентов объекта приведен на рис. 3.
Выходным результатом являются значения характеристик компонентов объекта.
Алгоритм работы в подсистеме будет следующий:
1. Ввод входных параметров.
2. Рассчитываются коэффициенты корреляции для каждого вида объекта;
3. На основе принципа максимума коэффициента корреляции выбирается наиболее подходящий компонент.
4. Вывод результата.
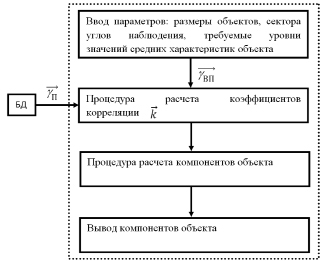
Рис. 3. Процесс функционирования подсистемы САПР средних характеристик объекта.
Использованы следующие обозначения: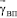 
– вектор, каждый из элементов которого являются соответствующие входные параметры; 
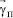– вектор, содержащий соответствующие зависимости в БД; 
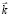– вектор, содержащий коэффициент корреляции.
Базируясь на основе приведенной модели в работе продемонстрирована возможность определения характерных размеров двумерного цилиндра, который дают максимальные средние значения ЭПР. Полученные результаты могут быть использованы при проектировании объектов, к которым предъявляются требования уменьшения уровня вторичного электромагнитного излучения.