Представление произвольно взятой функции с конкретным периодом в виде ряда называется рядом Фурье. Разложением по ортогональному базису называют данное решение в общем виде. Разложение функций в ряд Фурье является довольно мощным инструментом при решении разнообразных задач. Т.к. хорошо известны и изучены свойства данного преобразования при интегрировании, дифференцировании, а также сдвиге выражения по аргументу и свертке [3]. Человек, не знакомый с высшей математикой, а также с трудами французского ученого Фурье, скорее всего, не поймет, что это за «ряды» и для чего они нужны. Данное преобразование Фурье очень плотно вошло в нашу жизнь. Им пользуются не только математики, но и физики, химики, медики, астрономы, сейсмологи, океанографы и многие другие.
Ряды Фурье используются при решении многих прикладных задач. Преобразование Фурье можно проводить аналитическими, числительными и другими методами. Такие процессы как океанские приливы и световые волны до циклов солнечной активности относятся к числительному способу разложения любых колебательных процессов в ряд Фурье. Используя эти математические приемы, можно разбирать функции, представляя любые колебательные процессы в качестве ряда синусоидальных составляющих, которые переходят от минимума к максимуму и обратно. Преобразование Фурье является функцией, описывающей фазу и амплитуду синусоид, соответствующих определенной частоте. Данное преобразование используется для решения весьма сложных уравнений, которые описывают динамические процессы, возникающие под действием тепловой, световой или электрической энергии. Также ряды Фурье позволяют выделять постоянные составляющие в сложных колебательных сигналах, благодаря чему стало возможным правильно интерпретировать полученные экспериментальные наблюдения в медицине, химии и астрономии [1,5].
С ростом технологий, т.е. появление и развития компьютера, вывело преобразование Фурье на новый уровень. Данная методика прочно закрепилась практически во всех сферах науки и техники. В качестве примера можно привести цифровой аудио- и видеосигнал. Который стал наглядной реализацией роста научного процесса и применения рядов Фурье. Так, ряд Фурье в комплексной форме позволил совершить прорыв в изучении космического пространства. Кроме того, это повлияло на изучение физики полупроводниковых материалов и плазмы, микроволновой акустики, океанографии, радиолокации, сейсмологии [5].
Рассмотрим фазовый спектр периодического сигнала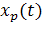 
определяется из следующего выражения:
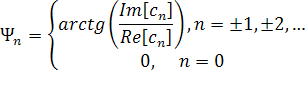
где символами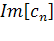 
и 
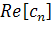соответственно обозначены мнимая и действительная части величины, заключенной в квадратные скобки.
Если 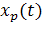умножить на действительную постоянную величину K, то разложение в ряд Фурье имеет следующий вид:
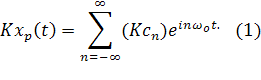
Из выражения (1) следует, что фазовый Фурье-спектр обладает следующими свойствами:
1) 
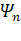является функцией 
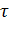, т. е. в отличие от спектра мощности, который не зависит от 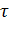, ,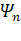 изменяется при сдвиге сигнала вдоль оси времени;
2)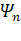 не зависит от К, т. е. 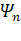инвариантен к усилению или ослаблению сигнала, в то время как спектр мощности является функцией К.
3) 
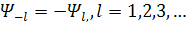т. е. 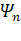является нечетной, функцией n.
Примечание. С учетом геометрической интерпретации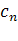 
приведенных выше рассуждений, 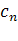можно выразить через спектр мощности и фазовый спектр следующим образом:
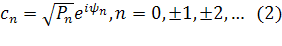
или
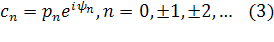
где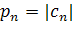 
и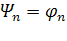 
.
Поскольку
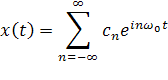
то из (2) и (3) следует, что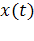 
может быть восстановлен однозначно, если известны амплитудный (или спектр мощности) и фазовый спектры.
Рассмотрим пример. Нам дана функция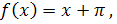 
на промежутке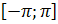 
Общий вид ряда Фурье:
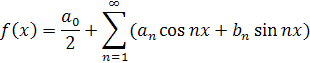
Найдем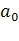 
:
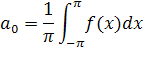
Подставим свои значения и получим:
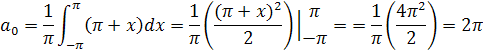
Найдем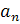 
:
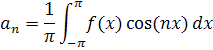
Подставим свои значения и получим:
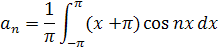
Используем замену:
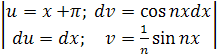
Получаем:
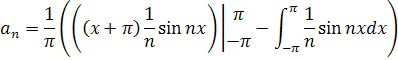
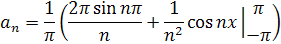
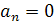
Найдем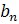 
по формуле:
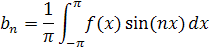
Подставим свои значения и получим:
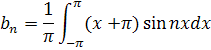
Используем замену:
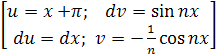
Получаем:
;
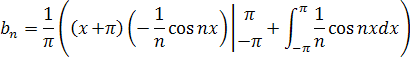
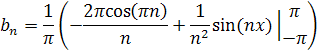
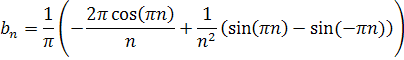
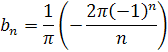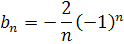
Общий вид функции:
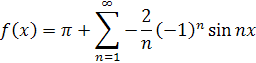
Найдем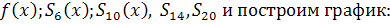 
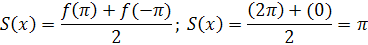
Максимальное значение суммы считается по формуле:
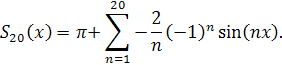
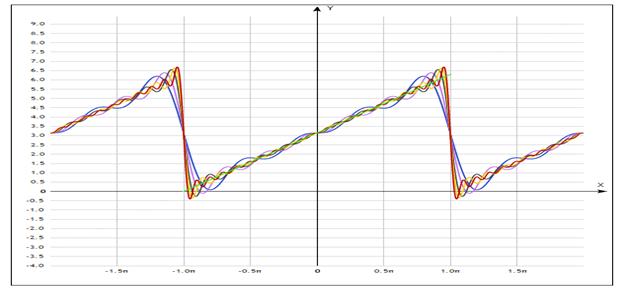
Вывод: несмотря на очень маленькие значения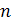 
для линейных функций, приближение осуществляется достаточно точно. И чем больше значение 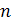, тем точнее график суммы ряда описывает данную функцию.