Новые образовательные стандарты отличаются тем, что главная цель сейчас – это личностный результат. Важна личность учащегося, а не сумма знаний по определённому предмету.
В ФГОСе под личностными результатами понимают психические новообразования, то есть качественные особенности психики, которые впервые появляются в данный возрастной период и определяют сознание ребенка, его отношение к среде, к внутренней и внешней жизни.
Таким образом, новые образовательные стандарты и, как следствие, новые цели и результаты обучения требуют организации исследовательской деятельности как неотъемлемой части образовательного процесса.
А. Н. Леонтьев дает следующее определение понятию "деятельность": деятельность – динамическая система взаимодействий субъекта с миром, в процессе которых происходит возникновение и воплощение в объекте психического образа и реализация опосредованных им отношений субъекта в предметной действительности [1, c. 208].
Л. Д. Ительсон [2, c. 674] деятельность определяет как внутреннюю (психическую) и внешнюю (физическую) активность человека, регулируемую сознаваемой целью.
Учебная исследовательская деятельность – это специально организованная, познавательная творческая деятельность учащихся, по своей структуре соответствующая научной деятельности, характеризующаяся целенаправленностью, активностью, предметностью, мотивацией и сознательностью, результатом которой является формирование познавательных мотивов, исследовательских умений, субъективно новых для учащихся знаний или способов деятельности [3, c. 122].
Исследовательская деятельность - это специфическая человеческая деятельность, которая регулируется сознанием и активностью личности, направлена на удовлетворение познавательных интеллектуальных потребностей, продуктом которой является новое знание, полученное в соответствии с поставленной целью и в соответствии с объективными законами и наличными обстоятельствами, определяющими реальность и достижимость цели [4, c. 45].
Целесообразно организовывать исследовательскую деятельность на уроках геометрии. Так как многие теоремы, рассматриваемые в школьном курсе, учащиеся могут доказать самостоятельно, главное правильно выдвинуть гипотезу и составить план исследования, в чем и поможет учитель.
Исследовательская деятельность подразумевает гибкость решения задачи и часто множественность ответов. Эти же особенности выделяют при использовании кейс-технологий.
"Кейс-технология" в переводе с английского означает описание конкретной ситуации, методический прием обучения.
Поэтому при обучении решению исследовательских задач целесообразно использовать ИКТ технологии, метод проектов, а также кейс-технологии.
Рассмотрим некоторые примеры.
Задание 1
Учащимся предлагается после изучения теоремы Пифагора решить следующий кейс.
Цель: доказать виновность или невиновность подозреваемого.
Ситуация: квартиру простого жителя Омска обокрали. Он написал заявление в полицию, о том, что его обокрали, разбив окно. Следователь приехал на место происшествия и обнаружил, что подоконник находится на расстоянии 520 см от земли. Поверхность земли на расстоянии 230 см от стены здания покрыта травой, на которой нет никаких повреждений и следов тоже нет. Не было найдено ни лестницы, ни веревки, никаких других предметов, которые бы помогли забраться в окно.
Учащиеся с помощью теоремы Пифагора должны прийти к выводу, что кража, скорее всего, инсценирована, так как человек не может подпрыгнуть примерно на 568 см без каких-либо приспособлений.
Возможно, у учащихся возникнут предположения, что вор пробрался через соседние окна, но об этом ничего не сказано, а значит и виновность еще не доказана.
Задание 2
На чемпионате мира по хоккею 2018 года, который пройдет в Дании, рекламное агентство выкупило часть хоккейной площадки от синей до лицевой линии для размещения рекламы (рисунок 6). При этом два круга сбрасывания диаметром 900 см дороже оставшейся зоны на 50 тыс. руб. за каждый квадратный метр. Какова стоимость всей выкупленной площадки, если цена основной зоны 100 тыс. руб. за 1 м2?
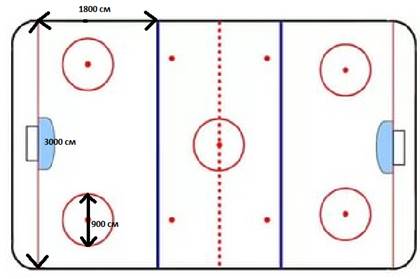
Рис. 1 - Хоккейная площадка
Задание 3
В восьмом классе после изучения темы "Площадь" целесообразно провести обобщение и систематизацию материала. Для этого учащимся можно предложить кейс.
Проблема: Вы бригадир строительной команды. Вам необходимо выложить сарафан на кухне длиной 5 метров и шириной 1,2 метров. У вас есть плитки в форме ромба, параллелограмма, трапеций и прямоугольных треугольников. Размеры плиток известны, они представлены на рисунке 2. Сколько плиток вам понадобится, и какой формы, если заказчик хочет, что бы все четыре вида плиток были использованы?
Задача имеет несколько решений. Также можно указать цену каждой плитки и предложить рассчитать самый выгодный вариант оформления фартука на кухне. Особенность данной задачи заключается в том, что учащиеся должны понять, что в уголках должны быть треугольники, иначе фартук выложить будет невозможно. Задачу лучше учащимся предложить в качестве домашнего задания.
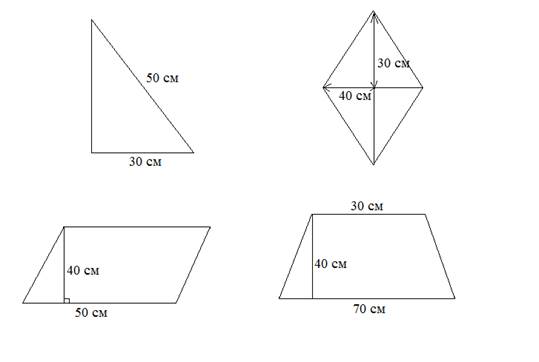
Рис. 2 – Размеры плиток
Задание 4
При изучении признака прямоугольника учащимся можно предложить в программе "Живая геометрия" построить параллелограмм, у которого диагонали равны. После чего измерить все углы параллелограмма и заполнить таблицу 1.
Таблица 1–Результаты измерения углов параллелограмма
|
∠A |
∠C |
∠B |
∠D |
Учащиеся должны заменить, что все четыре угла прямые и предположить, что данный параллелограмм - прямоугольник. Доказать данную гипотезу поможет учитель.
Задание 5
При изучении свойств ромба учащимся можно предложить поработать с программой "Живая геометрия". Необходимо построить ромб и провести диагонали, как на рисунке 3.
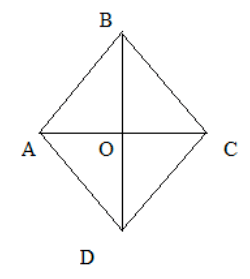
Рис. 3 - Ромб
После этого необходимо заполнить таблицу 17
Таблица 2 – Результат измерения углов
|
∠AOB |
∠ABO |
∠OBC |
∠BCO |
∠OCD |
∠CDO |
∠ODA |
∠DAO |
∠BAO |
Гипотеза: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Данная гипотеза доказывается учащимися.
Задание 6
При изучении темы: "Площади многоугольников" учащиеся еще не знают всех формул, необходимых для их нахождения, но свойство о том, что если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, изучается в самой начале изучения главы "Площадь"
Ученикам целесообразно предложить начертить в программе "Живая геометрия" произвольный четырехугольник и разбить его на пять разных фигур, например, как на рисунке 4 и заполнить таблицу 3, используя встроенную функцию программы "Нахождение площади фигуры".
Гипотеза: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
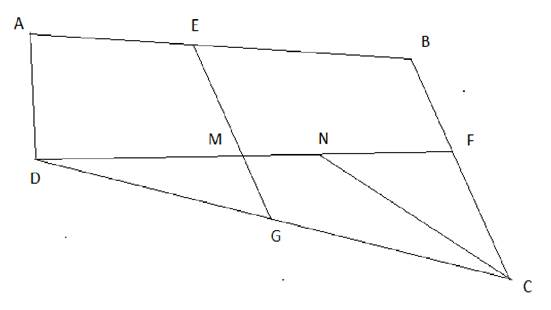
Рис. 4 – Произвольный четырехугольник
Таблица 3 – Площадь произвольной фигуры
|
SABCD |
SDAEM |
SMEBF |
SDMG |
SGMNC |
SNFC |
SDAEM+SMEBF+SDMG+SGMNC+SNFC |
Задание 7.
При изучении теоремы обратной теореме Пифагора учащимся можно предложить в программе GeoGebra построить такой треугольник, у которого квадрат одой стороны равен сумме квадратов двух других сторон. После этого предложить измерить все углы полученного треугольника. Размеры сторон учащиеся выбирают сами, например 3 см, 4 см и 5 см или 10 см, 6 см, 8 см. После измерения углов треугольника учащимся предлагается заполнить таблицу 4.
Таблица 4 – Градусная мера углов треугольника
|
∠A |
∠C |
∠B |
Учащиеся выдвигают гипотезу, что треугольник, у которого квадрат одной стороны равен сумме квадратов двух других сторон, является прямоугольным.
Задание 8
При изучении темы "Касательная к окружности" целесообразно использовать программу "Компас". Это одна из немногих программ, которая позволяет построить касательную через заданную точку кривой.
Учащимся предлагается построить окружность и провести радиус ОА. После провести касательную через точку А, как на рисунке 5.
Измерить угол, которые образует радиус, проведенный в точку касания и касательная.
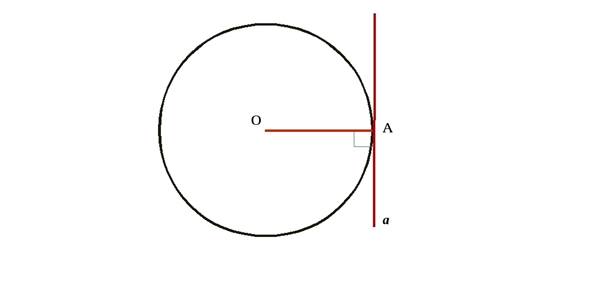
Рис. 5 – Касательная к окружности
Ученики выдвигают гипотезу о том, касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Таким образом, организация исследовательской деятельности в процессе обучения геометрии не только мотивирует учащихся и вызывает интерес к данной дисциплине, но и учит самостоятельно выдвигать гипотезы, доказывать их или опровергать, решать исследовательские задачи, используя знания по геометрии.

