Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Ключевым и самым распространенным показателем функционирования всей экономической системы страны является ВВП. Именно изменения ВВП декларируются главами государств и правительств в качестве результатов своей деятельности. Также ВВП служит в качестве мерила именно уровня развития национальных экономик, сравнения эффективности экономических систем разных государств и определения уровня жизни их граждан. Измерение динамики экономических изменений в жизни того или иного государства происходит благодаря исчислению темпов роста или падения ВВП. Экономическая теория предлагает два подхода по определению ВВП: по расходам и по доходам [1]. Первый подход математически может быть представлен как 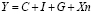, где Y – ВВП, С – потребление домашних хозяйств, I – инвестиции, G – госрасходы и Xn – чистый экспорт.

Однако следует учитывать, что ВВП является комплексным макроэкономическим показателем, поэтому с помощью его можно увидеть достаточно обобщенную картину. Использование ВВП в качестве инструмента анализа изменений в уровне и качестве жизни населения может предполагать ситуацию, когда при росте данного показателя, реальные доходы населения будут оставаться на прежнем уровне или даже снижаться. Таким образом, перед представителями экономической науки встает необходимость поиска агрегированных показателей, которые дополняя ВВП, могли бы более достоверно демонстрировать изменения качества жизни.

В качестве показателя, способного проиллюстрировать такие изменения рассматривается объем платных услуг населению. Именно этот статистический показатель является одной из двух составляющих потребления домашних хозяйств, следовательно, и ВВП. Совокупный спрос, измеряющий уровень потребления домашних хозяйств, формируется в рамках агрегирования показателей объема рынка товаров и рынка услуг. При этом, рынок услуг представляется намного более эластичным при изменении доходов населения, чем рынок товаров. Объясняется это, главным образом, тем, что склонность к потреблению услуг при падении реальных доходов населения сокращается значительно быстрее, чем аналогичный показатель на рынке товаров. В то же время, в постиндустриальном обществе сфера услуг играет все более значительную роль и по объемам не уступает рынку товаров. Таким образом, объем платных услуг является одним из наиболее подходящих инструментов для измерения уровня жизни населения. Использование данного показателя способно сформировать картину изменений социально-экономического положения страны и ее граждан. В общем случае, рост объема платных услуг соотносится с ростом доходов населения, с благоприятными изменениями уровня жизни. Падение же объема платных услуг способно сказать о сокращении доходов населения и падении склонности к потреблению. В связи с тем, что статистический показатель «Объем платных услуг населению» отражает объем потребления гражданами различных видов услуг, оказанных им за плату, то при его изучении необходим еще один показатель – это денежные доходы населения, которые отражают возможность населения тратить деньги на что-либо.

Таким образом, построим эконометрическую модель, где эндогенной переменной Vt является объем платных услуг населению. Объем платных услуг линейно зависит от достигнутого объема в предыдущем месяце, это подтверждает диаграмма рассеяния (рис. 1).

Тогда предопределенной переменной будет являться лаговая эндогенная переменная Vt-1. Как уже говорилось ранее, на объем платных услуг оказывают влияние денежные доходы населения, что также подтверждается диаграммой рассеяния на рис. 2. Обозначим их Xt. Чтобы учесть воздействие неучтенных факторов на эндогенную переменную, отразим их в уравнении модели как случайные остатки ut 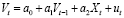(1):

(1)

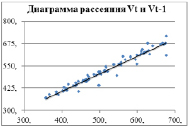
Рис. 1. Диаграмма рассеяния Vt и Vt-1

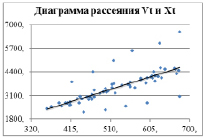
Рис. 2. Диаграмма рассеяния Vt и Xt

Зависимость объема платных услуг t-месяца от предыдущего (t–1) прямая, поэтому значение коэффициента a1 будет больше нуля; так как домашние хозяйства тратят только часть своего дохода на платные услуги, то коэффициент a2 будет в промежутке от нуля до единицы: a–1>0 , 0< a–2<1.

Оценка эконометрической модели (1), которая представляет линейную множественную регрессию, производится с помощью схемы Гаусса-Маркова [2]. Теорема Гаусса-Маркова имеет четыре предпосылки, две из которых входят в состав спецификации модели [3]:

При каждом фиксированном значениях предопределенной Vt-1 и экзогенной Xt переменных случайные возмущения (случайные остатки) ut имеют нулевое математическое ожидание: .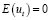

Средний квадрат разброса значений ut вокруг нуля остается неизменным при любом фиксированном значении предопределённой Vt-1 и экзогенной Xt переменных: .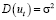

Тогда спецификация эконометрической модели выглядит следующем образом:

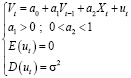
Статистическая информация представлена выборкой n=71, где периодичность ежемесячная с января 2010 года по декабрь 2015 года. Источник – Федеральная служба государственной статистики [4]. Оценку коэффициентов эконометрической модели (1) проведём с помощью метода наименьших квадратов, при условии, что предпосылки теоремы Гаусса-Маркова выполняются, используя функцию ЛИНЕЙН в Excel (см. таблbwe).

Результат использования функции ЛИНЕЙН

Полученные значения коэффициентов регрессоров соответствует двум условиям из спецификации. Представим оцененную эконометрическую модель:

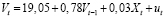
(7,675) (0,022) (0,002) (10,885)

Анализ качества спецификации модели (посредством определения значения коэффициента детерминации R^2 и проведения F-теста) выявил, что качество регрессии удовлетворительно, а именно регрессоры в рамках линейной модели обладают способностью объяснять значения эндогенной переменной Vt. В частности, согласно таблице значение R^2 равно 0,986, что означает, что значения vi переменной Vt на 98% объясняются в выборке значениями vi-1 регрессора Vt-1 и значениями xi регрессора Xt. Однако в связи с тем, что ESS и TSS – это случайные величины, то значение R^2 также случайный характер. F-тест определил, что гипотезу о том, что Vt-1 и Xt не влияют на Vt, принять нельзя.

Использование метода наименьших квадратов предполагает проверку оцениваемой модели на соответствие ряда ключевых условий, важнейшими из которых являются предпосылки теоремы Гаусса-Маркова. Проверка второй и третьей предпосылок теоремы Гаусса-Маркова выявила, что случайный остаток в модели гомоскедастичен и систематическая связь между значениями случайного члена в любых двух наблюдениях отсутствует. Это подтверждают проведённый тест Голдфелда-Квандта, и использование h-статистики Дарбина [5], которая подтвердила, что гипотезу об отсутствии автокорреляции принимаем, так как значение h = 1,815 не превышает на 5%-уровне значимости 1,96.

Эконометрические модели предназначены для объяснения и прогноза текущих значений эндогенных переменных по заданным значениям предопределенных переменных. Модель именуется адекватной, если прогнозы значений эндогенной переменной согласуются с ее наблюденными значениями. Таким образом, прогнозы используются и в процедуре проверки адекватности данной модели. Интервальный прогноз показал, что модель адекватна, так как значение эндогенной переменной из контролирующей выборки попало в эти интервалы: 536,96 < 558,3 < 580,27 ; 718,06 < 718,8 < <765,99.

Обратим внимание, что значение у последней эндогенной переменной очень близко к минимальной границы доверительного интервала, в отличие от первой. Это объясняется тем, что случайное возмущение последней очень большое, а первой – маленькое.

Проведенный анализ модели на адекватность и качественность подтверждает, что данную модель можно использовать в реальных условиях для определения объема платных услуг населения в зависимости от достигнутой его величины в прошлом месяце и от денежных доходов населения. Отметим, что в условиях собранной статистической информации при увеличении лагового эндогенного показателя Vt-1 на 1 млрд. рублей объем платных услуг в среднем примерно увеличится на 77,8 млн. рублей, а увеличение денежных доходов населения на 1 млрд. рублей увеличит объем платных услуг только на 2 миллиона рублей.