Сплавы на основе благородных металлов имеют особую популярность в стоматологии, поскольку в отличие от неблагородных сплавов они не токсичны, обладают высокой коррозионной стойкостью в условиях полости рта человека и не оказывают сенсибилизирующего действия. Для достижения необходимых технологических характеристик золотаи серебра их легируют неблагородными металлами. В данном случае используются медь, повышающая прочность сплавов, и индий, снижающий температуру плавления и улучшающий характеристики литья [1,2].
Уже достаточно давно хорошо изучены двойные системы трехкомпонентных сплавов золота, меди и индия Au-Cu-In и Ag-Au-In [3–7].
Сплавы для исследования выплавлялись из металлов высокой степени чистоты:
• золото – гранулы (99,92 %);
• серебро – гранулы (99,95 %);
• медь – проволока (99,9 %);
• индий полупроводниковой чистоты (99,999 %).
Образцы готовили в дуговой печи с нерасходуемым вольфрамовым электродом в атмосфере аргона на охлаждаемом поддоне. Полученные образцы отжигали в печах сопротивления при 500 оС в вакуумированных кварцевых ампулах в течение 1200 ч. Сплавы закаляли в холодной воде.
Исследование отожженных образцов проводили с помощью методов физико-химического анализа: рентгенофазового, микрорентгеноспектрального и электронной микроскопии.
Количественное содержание элементов в фазах и микроструктуру образцов исследовали на приборе «LEO EVO 50 XVP», снабженным энергодисперсионным анализатором «Inca Energy 450 (Oxford instruments)» при 15 кВ. Рентгенофазовый анализ (РФА) проводили методом порошка на дифрактометре «ДРОН-4» с использованием CuKα1–излучения.
Система Ag–Au–In при 500 °C характеризуется наличием области непрерывного твердого раствора с ГЦК структурой на основе золота и серебра, растворимость индия в котором закономерно увеличивается при увеличении содержания серебра. ς -Фазы двойных систем тоже образуют непрерывный твердый раствор. Растворимость серебра в α1–фазе, согласно результатам исследований составляет не менее 15 ат. %.
Система Au-Cu-In при 500°C имеет область гомогенности непрерывного твердого раствора на основе ГЦК-компонентов, растворимость индия в котором растет и достигает 15 ат. %, что выше, чем в двойных граничных системах. Растворимость меди в гексагональных фазах системы Au-In различна: в ς-фазе она составляет 13 ат. %, а в α1–фазе на привышает и 2 ат. %. Растворимость золота в фазах двойной системы Cu-In также различна: в ς-фазе – 9 ат. %, а в η′-фазе – 31 ат. %. Фаза γ, которая устойчива в системе Au-In существует при более низкой температуре, а в системе Cu-In при более высокой, имеет протяженную область гомогенности на изотермическом сечении.
В дополнение к эксперименту нами было проведено термодинамическое моделирование тройных систем методом CALPHAD.
«CALPHAD-метод» (CALculationofPHAseDiagrams) – это метод полуэмпирического моделирования фазовых равновесий. Согласно этому методу для каждой фазы проводится построение описания зависимости ее термодинамических свойств (к примеру, энергии Гиббса) от давления, температуры, состава, и других внешних параметров. После этого происходит расчет фазовых равновесий с использованием полученных описаний.
Для моделирования мы использовали описания двойных граничных систем из литературы, которые в дальнейшем экстраполировали на трехкомпонентную систему.
При моделировании системы Ag–Au–In нами была протестирована модель Муггиану, поскольку она является наиболее распространенной в практике расчетов многокомпонентных систем. Была сделана попытка рассчитать с использованием этой модели равновесия с участием расплава, ς- и ГЦК-фаз. Фаза α1 на этом этапе была исключена из рассмотрения, т.к. ее область гомогенности невелика. Выполненный расчет показал, что экстраполяция литературных описаний расплава, ГЦК и ς-фаз методом Муггиану дает неудовлетворительный результат (рис. 1). В частности, вместо единой области гексагональной ς-фазы на рассчитанной диаграмме возникают две несвязанные области. Варьирование единственного неизвестного параметра L(hcp, Ag, Au;0) в гексагональной фазе ς не позволяет улучшить результат.
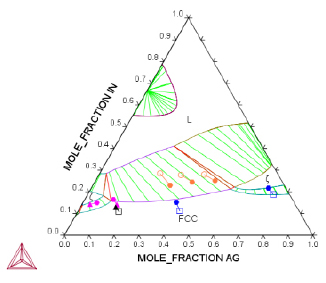
Рис. 1
В литературе [8, 9, 10] отмечалось, что для систем типа M1–M2–X (M1 и M2 – переходные или благородные металлы, принадлежащие к одной и той же группе периодической системы, X – неметалл или непереходный металл) термодинамические свойства разбавленных по X растворов количественно предсказываются с помощью модели [11], практически идентичной экстраполяционной формуле Тупа. Поэтому на следующем этапе был испытан этот вариант предсказания.
Расчеты по этому методу были выполнены с учетом всех трех неупорядоченных фаз: fcc, ς и α1. Результаты представлены на рис. 2.
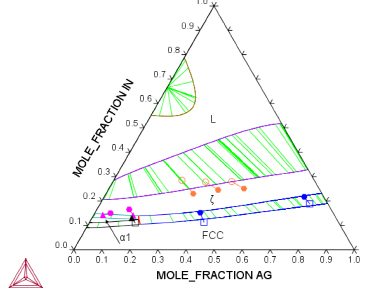
Рис. 2
Особенность системы Au-Cu-In заключается в том, что в граничных двойных системах Au-In и Cu–In устойчивы фазы с различной кристаллической структурой: в первой – гексагональные α1 (типа Nd) и ς (типа Mg), а во второй – орторомбическая δ типа Cu7In3 и гексагональная η′ типа Ni2In. Одинаковую структуру в обеих граничных системах, помимо ГЦК-твердого раствора, имеют только фазы со структурой γ-латуни.
Поэтому для построения полного термодинамического описания этой системы необходимо определить значения большого числа параметров: энергий Гиббса виртуальных фаз δ и η′ в системе Au-In, а также фаз α1 и ς в системе Cu-In. Кроме того, так как растворимости третьих компонентов в твердых растворах значительны, необходим учет параметров взаимодействия компонентов. Оценка такого большого числа параметров с использованием только данных по фазовым равновесиям невозможна и требует привлечения дополнительных данных, например, неэмпирических расчетов.
В связи с этим было принято решение ограничиться ориентировочным расчетом, в котором были учтены только ГЦК-твердый раствор и граничащие с ним фазы ς и γ-латунь. Корректное описание этих фаз позволяет воспроизвести основные черты фазовых равновесий в этой системе.
Поскольку модель Тупа в системе Ag–Au–In показала хороший результат, было решено использовать ее для описания ГЦК-твердого раствора и ς-фазы и в системе Au–Cu–In. Результаты расчета фазовых равновесий представлены на рис. 3.
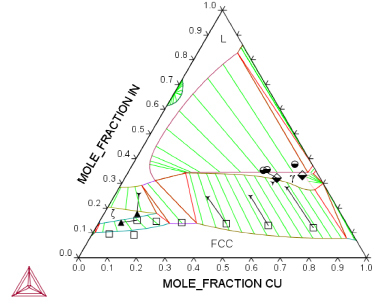
Рис. 3

