В начале XX века развиваются новые методы исследования, в основе которых положены методы функционального анализа. В частности приложение теории линейных операторов в различных банаховых пространствах к задаче моделирования реальных процессов с помощью дифференциальных уравнений и их систем особенно актуально в последние десятилетия при изучении явлений природы, решении многих задач физики, химии, биологии и других наук. Операторный метод позволяет реализовать функционально-аналитический подход к решению дифференциальных уравнений в конкретном банаховом пространстве. В основу статьи положены теоретические аспекты решения операторных уравнений, вида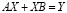 
, где А, В, Y – заданные операторы. Вопросы разрешимости таких уравнений в математической литературе были изучены для различных видов операторов А и В. Например, в [2] для операторов типа Романовского с частными интегралами в пространстве непрерывных функций, в [1] в общем случае для операторов, действующих в комплексном банаховом пространстве.
Цель нашего исследования состоит в изучении поведения решений эволюционных уравнений (т.е. уравнений, описывающих процессы, развивающиеся во времени), приложение теории эволюционного оператора для решения задачи Коши и задач из различных областей естествознания.
Остановимся на рассмотрении дифференциального уравнения
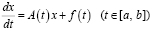(1)
с переменными оператор-функцией A(t) и вектор-функцией f(t), зависящими от вещественного параметра t, и методе его решения, разработанном в [1]. Там же приведены условия существования и получен общий вид решения задачи Коши в операторной форме.
Следует отметить, что существование решений однородного дифференциального уравнения
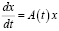
с начальным условием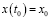 
в банаховом пространстве исследуется для случая, когда функции f(t) и A(t) сильно измеримы и интегрируемы по Бохнеру на конечных интервалах. Здесь же получено решение задачи Коши в операторной форме:
,
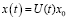где U(t) – эволюционный оператор, имеющий в общем случае вид
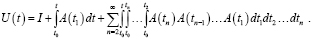
Здесь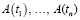 
– функции сильно интегрируемые, 
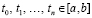, а интегрирование ведется по Бохнеру [1].
Решение задачи Коши для неоднородного уравнения (1) с начальными условиями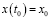 
приводит так же к необходимости введения эволюционного оператора, но уже в операторной форме 
.
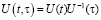Свойства оператора U(t,τ) рассмотрены в [1] и непосредственно вытекают из определения оператора:
а)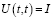 
,
b)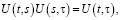 
c)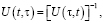 
d)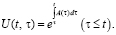 
При помощи эволюционного оператора решение задачи Коши для неоднородного уравнения (1) имеет вид
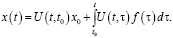
Примеры некоторых задач на нахождение решений дифференциальных уравнений, решение задач физики, химии, биологии и других естественных наук с использованием эволюционного оператора приводились в статье [3].
В качестве примера использования эволюционного оператора рассмотрим задачу
Задача 1. Цилиндрическая катушка изготовлена из медной проволоки. При прохождении через катушку электрического тока выделяется теплота. Построим математическую модель описанного физического процесса и выведем формулу для температуры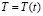 
установившегося режима как функции времени t.
Решение.
Пусть T0 – температура среды, в которой находится катушка;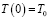 
; с – удельная теплоемкость меди; γ – ее плотность; V – объем; S – площадь поверхности катушки; q – количество теплоты, выделяемое на протяжении единицы времени; k – коэффициент теплопроводности.
Количество теплоты, выделяющееся за время Δt, равно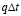 
. Эта величина состоит из двух частей: теплоты, которая идет на повышение температуры ΔT, и теплоты, уходящей в среду, окружающую катушку. Первая часть равна 
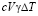, а вторая 
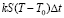(количество этой теплоты пропорционально разности температуры T и T0 катушки и среды, а также величинам S и Δt); отсюда 
.
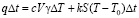Разделив обе части последнего равенства на Δt и переходя к пределу при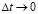 
, получим дифференциальное уравнение
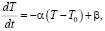
где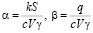 
.
Здесь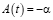 
, 
.
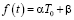Найдем U(t):
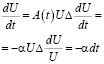
Отсюда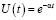 
.
Найдем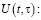 
,
.
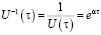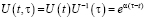Тогда
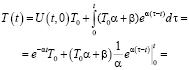
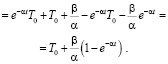
Подставляя α и β получим
–
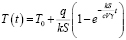искомая функция.
Рассмотренный метод может использоваться в качестве дополнения к классическим приемам решения линейных дифференциальных уравнений первого порядка. Более общий случай, когда A(t) является линейным оператором, требует дополнительных знаний из области функционального анализа.
Приведем пример задачи, которая также может быть решена с использованием эволюционного оператора. Поставим цель провести исследование на устойчивость с использованием фазового портрета.
Задача 2. Рассмотрим простой маятник в случае, когда сила трения не учитывается. В этом случае уравнение маятника без учета силы трения имеет вид:
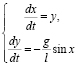
и является консервативной в том смысле, что, если маятнику сообщено начальное ускорение, то он продолжит бесконечные колебания, что нереалистично.
Положение равновесия маятника будет наблюдаться в точках (пπ; 0), где n = 0, ±1,±2… Фазовый портрет этой системы для частного случая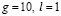 
получен с помощью компьютерного моделирования.
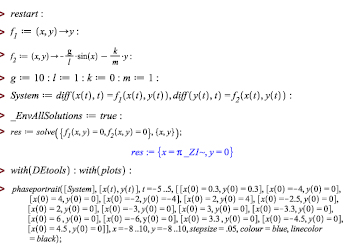
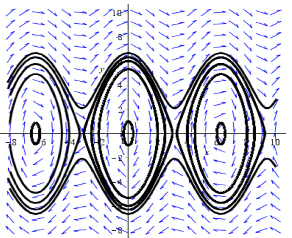
Анализируя построенный фазовый портрет, можно сделать следующие выводы:
• траектории в окрестности точек равновесия (0;0), (2π;0) и (-2π;0) и т.д. демонстрируют качественное поведение, характерное для траекторий в окрестности центра;
• траектории в окрестности точек равновесия (π;0) и (-π;0) и т.д. демонстрируют качественное поведение, характерное для траекторий в окрестности седловой точки.
Выполним проверку, выполнив расчёты для нахождения собственных чисел якобиана, вычисленного в точках (0;0) и (π;0):
Так как в точке равновесия (0;0) якобиан имеет собственные числа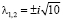 
, то эта точка является устойчивым фокусом. В точке (π;0) собственные числа якобиана равны 
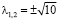. Поэтому (π;0) – седловая точка.
Таким образом, качественное исследование точек равновесия простого маятника может быть проведено с помощью построения фазового портрета и с использованием соответствующей линеаризованной модели.