Когда осуществляют анализ и синтеза комплексных электродинамических систем, требуется весьма точным образом проводить учет возникающих в них физических процессов.
Основные свойства для большого числа вариантов весьма быстро меняются при изменении длин волн, а также поляризаций и углов, под которыми идет падение радиоволн. С тем, чтобы проводить изучение ключевых свойств объектов для некоторого диапазона длин волн и разных углов наблюдения, требуется применять или специальные антенные полигоны, или безэховые камеры. Стоимость подобных сооружений может быть значительной [1].
Поэтому, исследователям приходится использовать способы математического моделирования [2].
Для средств вычислительной техники в течение последних лет наблюдаются большие изменения. В настоящее время применяют многоядерные процессоры, дающие возможности для того, чтобы код выполнялся многопоточным образом.
Проведение обслуживания интерфейсов идет в отдельных потоках, а данные обрабатываются при помощи другого. Помимо этого обработка различных потоков может происходить для разных процессоров одновременным образом, что реально обеспечивает рост скоростей вычислений.
В последнее время по всему миру происходит усиление внимания к применению высокопроизводительных вычислительных ресурсов.
С одной стороны, происходит рост числа пользователей в персональных миникластерах, с другой идут процессы концентрации мощных вычислительных ресурсов, которые располагаются относительно центров коллективного пользования и развивается инфраструктура удаленного доступа при использовании телекоммуникационных средств.
При этом в существующих условиях многие исследователи понимают что последующее повышение производительности в компьютерах только вследствие того, что будут улучшаться характеристики электронных элементов, имеет некоторый предел, который определяется законами физики.
Дальнейший рост производительности может быть только вследствие того, что будут распараллеливаться процессы обработки информации. Но исследователи столкнулись с проблемами при построении параллельных вычислительных процессов, ведущих к обеспечению достижения максимальной производительности.
Уменьшение времени исполнения больших объемов работ на основе разбиения по отдельным работам, которые можно выполнять независимым и одновременным образом, применяется во многих сферах деятельности.
В сфере вычислительной техники это может быть достигнуто на основе того, что увеличивается количество одновременно функционирующих процессоров. Но при этом известно, что при переносе обычных программ на объекты многопроцессорных вычислительных систем может не привести к ожидаемому выигрышу в производительности. Это даже может привести к тому, что после такого переноса программы будут работать медленнее.
Основываясь на опыте исследователей, можно сказать, что сформировать эффективные параллельные программы или использовать уже существующую последовательную программу в параллельных вычислениях весьма трудно.
Это определяется тем, что при переходе к применению многопроцессорных систем нам приходится сталкиваться с принципиально новым содержанием. При этом очень важным будет проведение структурного анализа алгоритмов, выявление особенностей их внутреннего параллелизма. Осуществление такого анализа требует, чтобы было глубокое понимание существа проблем.
Во многих случаях проблема состоит в том, что программисты не совсем ясно понимают алгоритмы решения задач, а математики не могут поправить программы, поскольку не обладают достаточной квалификацией в сфере программирования. Такую трудность можно преодолеть, если применять модель представления алгоритма, которая будет понятной как для математика, так и для программиста.
При этом математики и программисты могут функционировать в большой степени независимым образом, осуществляя взаимодействие только в рамках применяемой модели.
Организовать параллельные вычисления в параллельных компьютерах с общей памятью (мультипроцессорах) значительно проще, чем в системах, имеющих распределенную память. В таком случае нет необходимости думать о том, как распределять массивы.
Но компьютеры такого класса характеризуются небольшим числом процессоров и весьма высокой стоимостью. В этой связи обычно применяют разные решения, которые позволяют сделать увеличение числа процессоров, но при этом сохраняются возможности работ в рамках единых адресных пространств.
Например, общую память можно сделать физически распределенной, но при этом все процессоры будут иметь доступ к памяти в любом процессоре. Это может быть достигнуто на основе применения специальных программно-аппаратных средств. Приходится решать основную проблему, которая возникает – обеспечить когерентность кэш-памяти по отдельным процессорам.
В определенных ситуациях интерес представляет то, какие характеристики рассеяния систем не только на одной длине волны, а в диапазоне длин волн [3].
В работе проводится решение некоторых задач:
1. Идет разработка модели рассеяния радиоволн на объектах, имеющих произвольную форму [4];
2. Идет разработка алгоритма, связанного с численным решением задачи рассеяния радиоволн при помощи интегральных уравнений;
3. Идет разработка программной реализации алгоритма решения на базе интегрального уравнения при учете того, что распараллеливаются вычисления.
Применение интегральных уравнений обуславливает расчет токов, которые возникают на электродинамических телах. Подобный способ эффективным образом применяется при проведении расчетов характеристик рассеяния систем, относящихся к резонансной области. Когда увеличиваются размеры системы, происходит рост машинного времени, а также объемов оперативной памяти, которые требовались для процессов расчетов.
Когда программа запущена, идет создание нового процесса. Создаются дополнительные потоки, для выполнения фоновых задач. Каждому из потоков соответствует собственный стек, но системными ресурсами потоки применяются совместным образом.
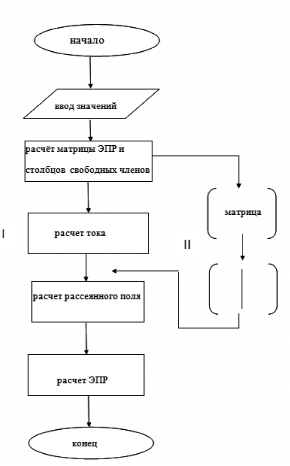
Рис. 1. Алгоритм расчета характеристик рассеяния
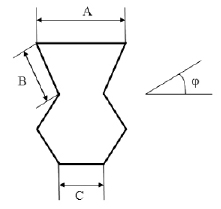
Рис. 2. Схема рассеяния электромагнитных волн на объекте
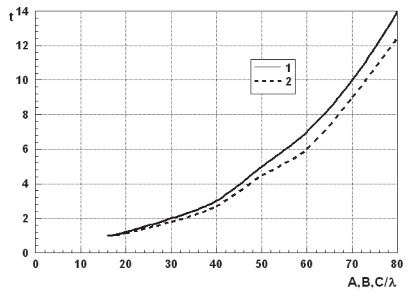
Рис. 3. Зависимость требуемого времени расчета в условных единицах в зависимости от длины контура объекта
На основе рассеивающих характеристик систем на одной длине волны можно осуществлять прогнозирование рассеивающих характеристик рассеяния по другим длинам волн, то есть, не надо делать реальный эксперимент.
Для уравнения Фредгольма первого рода, которое позволяет определять плотность требуемого электрического тока, когда рассматривается Е-поляризация [5] записывается выражение
,
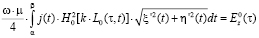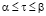, (1)
в нем
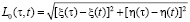
позволяет рассчитать расстояние между точкой наблюдения и интегрирования,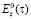 
– показывает продольную составляющую напряженности по электрическому полю в точке, которая находится на контуре. Задание контура происходит параметрическим образом:
,
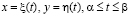а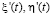 
– определяют первые производные по соответствующим функциям, 
, 
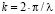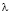– определяет длину электромагнитной волны.
При решении уравнения (1) методом моментов [6, 7] проводится дискретизация и оно приводится к системе линейных алгебраических уравнений, из которой определяются продольные электрические токи [8, 9] с плотностью
, 
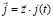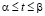, (2)
На рис 1. изображен алгоритм расчета характеристик рассеивания (эффективной площади рассеяния (ЭПР)). Римской цифрой I обозначен прямой ход без использования параллельности, римской цифрой II с использованием параллельных вычислений.
Вводятся исходные значения, и формируется матрица, матрица заполняется элементами, количество элементов матрицы зависит от размера матрицы. Размер матрицы зависит от числа дискретизации, поскольку количество дискретизаций велико, то и размер матрицы будет достаточно велик.
Отсюда следует, что время расчета данной матрицы будет возрастать в зависимости от количества элементов матрицы. Для того что бы уменьшить время выполнения расчётов мы применим метод распараллеливания вычислений путем создания потоков.
На этапе формирования матрицы импедансов, создаются новые потоки которые разделять данную матрицу на две части (для 2 ядерного процессора) и процесс формирования матрицы будит проходить в двух независимых потоках, что позволит эффективнее использовать вычислительную мощность ЭВМ, и получить выигрыш во времени, так как процесс вычисления будет происходить на двух ядрах.
На рис. 2 приведена схема рассеяния электромагнитных волн на объекте.
На рис. 3 дана зависимость требуемого времени расчета в условных единицах в зависимости от длины контура объекта. Общая длина контура L=A+2B+5C. Длина элементов контура варьировалась в следующих пределах: 2l≤A,B,C≤10l.