В зависимости углов падения радиоволн, когда они рассеиваются для весьма больших (если сравнивать размеры и длину волны) объектах, мы можем оценить характеристики разных электромагнитных явлений, например, связанных с бегущими и ползущими волнами, а также дифракционными эффектами для поверхностей и ребер [5]. Свойства численных способов, например подходов, применяющих интегральные уравнения, связаны с ограниченными электрическими размерами соответствующих объектов, а подходов, основанных на оптических методиках, – сложностью форм объектов. Гибридные методы, в которых объединяются численные, а также асимптотические методики, дают существенное усиление классов в анализирующих процедурах, связанных с рассеянием радиоволн, но отличие по гибридным способам, а, также асимптотическим и строгим, весьма условна. Те, которые рассматриваются как асимптотические способы, могут быть гибридными среди строгих интегральных описаний электромагнитных полей и геометрооптическими приближениями для токов на объектах.
В гибридных методах в первом приближении для общих объектах осуществляются процессы аппроксимации на основе множества обычных составляющих, а в общем решение проблем рассеяния рассматривается в виде суммы решений, известных для отдельных составляющих. Основным достоинством указанного подхода заключается в том, что для эффектов рассеяния на больших (с точки зрения сравнения с длиной волны) объектах мы можем проводить аппроксимацию, не прибегать к сложным расчетам. В качестве основного недостатка следует отметить то, что принимаются во внимание лишь рассеянные волны по нулевым («зеркальным») и первым порядкам и происходит пренебрежение теми, которые взаимодействуют с различными рассеивающими составляющими [2].
С тем, чтобы преодолеть подобные недостатки мы можем использовать два подхода:
1. Осуществление более точного учета по дифракционным эффектам на ребрах и искривленных поверхностях объектах на базе аналитических подходах, которые созданы на основе того, что объединяются способы классической оптики и применяют геометрическую и физическую теорию дифракции.
2. Для второго способа используют способ интегральных уравнений, в который базируется на теории линейных пространств, а также ортогональных проекций [3].
Кроме того, существуют возможности для того, чтобы формулировать общие необходимые условия для того, чтобы в гибридных подходах происходило сохранение эффективности для всех типов сложных объектов. Они состоят в том, что:
1. в высокоточных «исходных» решениях требуется, чтобы они были справедливы для тех же аргументов, что и для гибридного способа;
2. для низкочастотных областей (областей, где является эффективным методом моментов) требуется делать ее приблизительно на 1/2 от края поверхностей или от границ, соответствующим разделам участков непрерывности материалов объектов;
3. в гибридных способах получают приемлемые результаты по анализу характеристик рассеяния электрически больших объектов.
Важно отметить, что с использованием радиолокационных характеристик объектов при заданных частотах первичных радиоволн (получающихся при процессах математического моделирования или в эксперименте) можно проводить прогнозирование значений радиолокационных характеристик для частотных диапазонов [5]. Это может быть и для идеально проводящих объектов, и для содержащих магнитодиэлектрические материалы.
Мы проводили анализ возможностей использования комбинации метода интегральных уравнений и метода физической оптики для расчета характеристик рассеяния объекта, изображенного на рис. 1. На участке BC расчет проводится на основе метода физической оптики, а на участке BADC расчет проводится на основе метода интегральных уравнений. Задача состояла в том, чтобы определить связь между a и длиной контура La = 2(a(p + 1) + L), при которых будет значение средней эффективной площади рассеяния (ЭПР)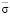 
, превышающее 20 дБ в заданном секторе углов.
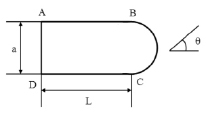
Рис. 1. Схема рассеяния электромагнитных волн на объекте
Функция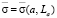 
является многоэкстремальной, в этой связи для ее расчетов приходилось применять метод сеток [1] при последовательном сужении области определяемых значений. По каждому из участков сетки использовался метод локальной оптимизации – метод золотого сечения [1].
На рис. 2 даны зависимости длины контура La от того, какой размер a для разных секторов углов наблюдения Δθ.
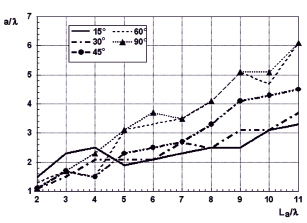
Рис. 2. Иллюстрация зависимости длины контура исследуемого La от размера a для сектора углов Δθ = 5 °, 15 °, 30 °, 45 °, 60 °, 90 °
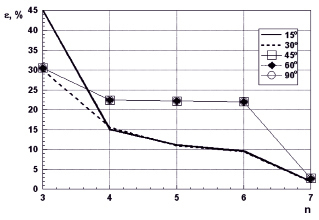
Рис. 3. Зависимость относительной ошибки от степени аппроксимирующего полинома
Была осуществлена аппроксимация рассчитанных зависимостей a от La на основе полиномиальных зависимостей, на базе метода наименьших квадратов [6]. Рис. 3 иллюстрирует зависимость того, какова относительная ошибка линейной аппроксимации от значения сектора углов наблюдения [7], когда степень полинома n изменяется от 1 до 4. Мы можем увидеть, что, что значение максимальной ошибки аппроксимации достигается, когда значение сектора углов наблюдения будет находится в пределах 0 ° ≤ Δθ ≤ 15 °. Хорошая с точки зрения практического использования аппроксимация (при относительной ошибке меньше чем 5 %) будет получаться при 30 ° ≤ Δθ ≤ 90 °, когда степень аппроксимирующего полинома будет n ≥ 3.