Задачи, касающиеся обработки рассеянных радиосигналов, в настоящее время имеют большое практическое значение [5]. Для объектов, на которые падают радиосигналы, имеющие разную частоту, можно отметить характерные отражательные возможности [3]. Возникают проблемы, которые связаны с особенностями распознавания рассеянных радиосигналов (идет их классификация, различение), то есть исследователи относят наблюдаемые тела к некоторым классам и типам [4].
В задачах, которые связаны с тем, что проводится распознавание радиосигналов, мы можем общие черты с аналогичными сложными задачами, направленными на распознавание изображений. Исходя из этого, мы можем проводить некоторые аналогии, которые связаны с процессами автоматизации распознавания болезненных симптомов в медицинских областях и в сфере распознавания радиосигналов. Когда идут процессы распознавания образов, то мы можем комбинировать радио информацию с данными, которые мы получаем для других диапазонов волн [4, 9].
Поскольку наблюдается большой интерес к обозначенной теме, возникают вопросы о том, на основе каких принципов осуществлять разработки эффективных алгоритмов, которые связаны с расчетами и прогнозированием радиоволн, которые рассеиваются на объектах.
Достоинством метода интегральных уравнений мы можем считать то, что компьютерные эксперименты вполне могут заменить натурные, при адекватном построении соответствующих моделей [1, 2].
Данные мы можем использовать не только при проведении анализа решений относительно прямых задач, но и когда проводятся исследования по возможностям того, чтобы были обозначены решения по обратным задачам, то есть, когда происходит определение форм объектов или отражающих свойств по их соответствующим поверхностям.
При проведении решения задач, которые связанных с процессами прохождения радиосигналов по каналам связи, необходимо, чтобы большое внимание уделялось тому, как идет изменение информационных параметров сигнала, поскольку это направлено на задачи, в которых стремятся к тому, чтобы максимальным образом сохранить информацию, которая переносится сигналами.
В таких случаях, когда информация закладывается в форму сигнала (обычно она достаточно простая), то в задачах, в которых целью является сохранение информации, стремятся к тому, чтобы была сохранена форма (или спектральные составляющие) сигналов.
Целью работы является построение алгоритма расчета и исследование возможности представления локальных источников изотропными отражателями.
В качестве модели рассмотрим объект, изображенный на рисунке. Объект состоит из двумерных цилиндров длиной a и шириной b, с расстоянием между ними L. На объект под определенным углом q падает электромагнитная волна. Значения размеров объекта варьировались в следующих пределах: 2l ≤ a, b, L ≤ 11l.
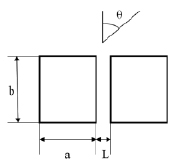
Схема рассеяния электромагнитных волн на составном объекте
При математическом моделировании характеристики рассеяния рассчитываются при помощи двух подходов:
1. Метод интегральных уравнений [3, 4]. На основе данного метода нами моделировались экспериментальные данные.
2. Подход, в рамках которого сложная дифракционная структура представлялась в виде суперпозиции элементарных отражателей, каждый из которых имеет свою характеристику рассеяния [4, 6].
Рассмотрим использование этих двух подходов. В первом подходе используется методика расчета характеристик рассеяния на основе метода интегральных уравнений, описанная в [5]. Расчет токов на поверхности (контуре) объекта для случая E-поляризации падающей электромагнитной волны проводится на основе решения интегрального уравнения Фредгольма 1-го рода.
Во втором подходе использовался алгоритм расчета характеристик рассеяния, основанный на представлении объекта в виде совокупности элементарных отражателей.
В рассматриваемой нами модели выделим следующие элементарные отражатели (рисунок): двумерные пластины, расположенные с левой и правой стороны, соответственно, клинья, образованные стыками пластин.
Расчеты на основе двух вышеизложенных подходов проводились для размеров структуры лежащих в резонансных пределах [6, 7]. Определялось значение сектора углов наблюдения локальные источники можно было представить изотропными источниками на основе сравнения значений моностатических эффективных площадей рассеяния (ЭПР), полученных с использованием двух рассмотренных подходов. Рассматриваемые особенности рассеяния можно встретить беспроводных сетях [8, 9].
В ходе машинного эксперимента было установлено, что для рассматриваемой модели для указанных размеров структуры локальные отражатели могут быть представлены изотропными источниками при углах наблюдения, лежащих в секторе от 40 ° до 57 °.

