В современном мире разнообразные математические модели активно используются учеными, экономистами, аналитиками и т.д. Всевозможные математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности и даже в исследовании политических процессов. С помощью этих моделей можно сформировать более полное понимание сущности происходящих в мире процессов.
Поскольку Российская Федерация является энергетической сверхдержавой с большими разведанными запасами нефти, природного газа и угля, то особенно актуальным вопросом для нашей страны стало рассмотрение таких математических моделей, в которых, так или иначе, присутствует переменная, связанная с продуктами нефтегазовой промышленности. В работе представлен анализ зависимости оптовых цен на бензин от полной себестоимости добычи (поставки) нефти.
На сегодняшний день одной единственной повсеместно использующейся математической модели, которая бы предлагалась для объяснения или прогноза оптовых цен на бензин не существует. В первую очередь, это связано с тем, что рассматривается большое количество разнообразных факторов, слабо или сильно влияющих на стоимость бензина. К таким факторам большинство экспертов относят: цены на нефть, курсы мировых валют, спрос и предложение на бензин, объемы добычи нефти, налоги и др.
В связи с тем, что мнения профессионалов в нефтегазовой промышленности, которые касаются определения основных факторов, формирующих цены на бензин, разделились, то каждому индивиду при рассмотрении математической модели необходимо самостоятельно выбирать предопределенные переменные для модели.
Определим, как основные факторы, влияющие на цены на бензин, стоимость сырья, из которого делается бензин, а также его транспортировка до поставщиков. Поскольку, показатель полной себестоимости добычи (поставки) нефти включает в себя указанные затраты, то небеспочвенным будет предположение, что себестоимость добычи (поставки) нефти имеет непосредственное влияние на средние оптовые цены на бензин. Согласно определению, «Полная себестоимость добычи (поставки) нефти – выраженные в денежной форме текущие затраты нефтедобывающей организации (отрасли) на разработку и эксплуатацию нефтяных месторождений, включая: буровые работы, управление движением жидкостей и газа в пласте к забоям эксплуатационных скважин, подъем жидкостей по стволу скважин на поверхность, движение нефти от устья скважин до нефтесборных пунктов и до пунктов сдачи потребителям» [5].
Рассмотрим конкретный пример, где за основу для расчётов был взят Московский регион и соответствующие для него данные средних оптовых цен на бензин АИ-95 операторов Московского региона по кварталам 2006-2016 гг., а также полную себестоимость добычи (поставки) нефти (таблица).
Статистическая информация для эконометрической модели»
|
Статистические данные для эконометрической модели |
||
|
Кварталы |
Средние оптовые цены на бензин АИ-95 операторов Московского региона, руб/т |
Полная себестоимость добычи (поставки) тонны нефти, руб. |
|
I кв. 2004 г. |
17 365 |
2 341,30 |
|
II кв. 2004 г. |
17 894 |
2 536,60 |
|
III кв. 2004 г. |
17 768 |
2 443,70 |
|
IV кв. 2004 г. |
17 915 |
2 532,20 |
|
I кв. 2005 г. |
17 984 |
2 563,30 |
|
II кв. 2005 г. |
17 980 |
2 539,10 |
|
III кв. 2005 г. |
17 548 |
3 371,30 |
|
IV кв. 2005 г. |
17 487 |
3 282,60 |
|
I кв. 2006 г. |
18 575 |
3 415,40 |
|
II кв. 2006 г. |
19 550 |
3 967,70 |
|
III кв. 2006 г. |
23 025 |
4 180,70 |
|
IV кв. 2006 г. |
19 475 |
3 851,80 |
|
I кв. 2007 г. |
17 450 |
3 724,50 |
|
II кв. 2007 г. |
21 650 |
4 227,80 |
|
III кв. 2007 г. |
22 225 |
4 692,80 |
|
IV кв. 2007 г. |
25 500 |
5 115,70 |
|
I кв. 2008 г. |
22 600 |
5 236,40 |
|
II кв. 2008 г. |
28 600 |
6 106,30 |
|
III кв. 2008 г. |
29 700 |
6 200,00 |
|
IV кв. 2008 г. |
18 400 |
4 169,00 |
|
I кв. 2009 г. |
18 750 |
3 663,20 |
|
II кв. 2009 г. |
25 150 |
4 277,70 |
|
III кв. 2009 г. |
27 950 |
4 977,70 |
|
IV кв. 2009 г. |
23 075 |
5 105,90 |
|
I кв. 2010 г. |
24 350 |
5 124,20 |
|
II кв. 2010 г. |
27 650 |
5 322,70 |
|
III кв. 2010 г. |
27 450 |
5 420,20 |
|
IV кв. 2010 г. |
27 675 |
5 838,10 |
|
I кв. 2011 г. |
28 325 |
6 411,30 |
|
II кв. 2011 г. |
33 067 |
6 815,30 |
|
III кв. 2011 г. |
34 832 |
7 007,20 |
|
IV кв. 2011 г. |
32 543 |
6 986,50 |
|
I кв. 2012 г. |
31 083 |
7 604,30 |
|
II кв. 2012 г. |
33 433 |
7 313,30 |
|
III кв. 2012 г. |
37 514 |
8 217,60 |
|
IV кв. 2012 г. |
34 617 |
8 273,10 |
|
I кв. 2013 г. |
32 743 |
7 987,20 |
|
II кв. 2013 г. |
32 186 |
7 945,40 |
|
III кв. 2013 г. |
39 800 |
8 405,20 |
|
IV кв. 2013 г. |
33 000 |
8 846,40 |
|
I кв. 2014 г. |
38 053 |
9 129,10 |
|
II кв. 2014 г. |
39 640 |
9 247,90 |
|
III кв. 2014 г. |
40 560 |
9 264,50 |
|
IV кв. 2014 г. |
41 293 |
8 756,20 |
|
I кв. 2015 г. |
41 387 |
10 296,50 |
|
II кв. 2015 г. |
43 040 |
10 852,30 |
|
III кв. 2015 г. |
45 227 |
10 354,90 |
|
IV кв. 2015 г. |
41 533 |
9 368,40 |
|
I кв. 2016 г. |
43 667 |
8 380,40 |
|
II кв. 2016 г. |
44 267 |
10 040,90 |
Примечание. Таблица составлена автором на основании статистических данных с официальных сайтов [1-4].
Таким образом, в модели рассмотрим следующие переменные:
1. Средние оптовые цены на бензин АИ-95 операторов Московского региона (руб/т). В модели оптовая цена является эндогенной переменной.
2. Полная себестоимость добычи (поставки) тонны нефти, руб. Себестоимость – предопределенная переменная.
Основная цель работы – построение модели парной регрессии на основе исходных статистических данных и проведение анализа данной модели на качественность, адекватность, соответствие условиям теоремы Гаусса-Маркова и возможность составление прогноза в рамках рассмотренной модели. Для реализации цели последовательно выполняются соответствующие этапы.
Составляем спецификацию линейной модели парной регрессии:
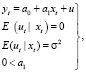
где yt – значения средних оптовых цен на бензин АИ-95 операторов Московского региона, xt – полная себестоимость добычи (поставки) тонны нефти, ut – случайная величина.
Выделим из данных контролирующую выборку:
|
II кв. 2006 г. |
19 550 |
3 967,70 |
|
III кв. 2007 г. |
22 225 |
4 692,80 |
|
II кв. 2009 г. |
25 150 |
4 277,70 |
|
I кв. 2010 г. |
24 350 |
5 124,20 |
|
II кв. 2013 г. |
32 186 |
7 945,40 |
Остальная часть массива – это обучающая выборка.
С помощью функции ЛИНЕЙН в MS Excel получим матрицу оценок параметров методом наименьших квадратов, где полная себестоимость добычи (поставки) тонны нефти составляет массив известных переменных X; средние оптовые цены на бензин АИ-95 операторов Московского региона – массив переменных Y. Получатся следующие результаты:
|
3,488277207 |
7461,005702 |
|
0,131267601 |
860,7872125 |
|
0,936353546 |
2292,414141 |
|
706,1661337 |
48 |
|
3711017851 |
252247804,5 |
Отсюда, оцененная модель имеет следующий вид:
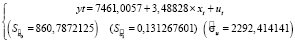
Значение коэффициента детерминации в рамках модели составляет 0,94. Так как, R2 > 0,8, то xt обладает сильным влиянием на yt, а значит, значения средних оптовых цен на бензин АИ-95 операторов Московского региона почти полностью объясняются значениями полной себестоимости добычи (поставки) тонны нефти.
Согласно использованным расчетам основные показатели для критерия Фишера таковы: F = 747,4601, а Fкр = F.ОБР.ПХ(0,05;1;48) = 4,042652. Т.к. неравенство F ≤ Fкр не выполняется, то можно сделать вывод о том, что качество регрессии удовлетворительно, регрессор в рамках рассматриваемой модели обладает способностью объяснять значения эндогенной переменной yt и спецификация модели качественная.
Поскольку после проведения теста Голдфелда-Кванта неравенства:
GQ = 0,5356 ≤ Fкрит = 2,0144
и
1/GQ = 1,8663 ≤ Fкрит = 2,0144
справедливы, то нет основания полагать, что предпосылка о гомоскедастичности случайного остатка в модели неадекватна. В данном случае случайные остатки в модели гомоскедастичные.
В результате проведения теста Дарвина-Уотсона получилось, что значение показателя статистики DW = 1,6841 попало в подмножество М3 = (du; 4-du) = (1,59; 2,41), и гипотеза Н0: Cov (ui; uj) = 0 при j = i-1 адекватна. Отсюда, следует, что в рассматриваемой эконометрической модели оценки параметров получены несмещенные и эффективные.
На основании проведенной проверки модели на адекватность и способность к прогнозированию значений эндогенных переменных по оцененной эконометрической модели установлено, что все значения эндогенных переменных из контролирующих выборок попали в соответствующие доверительные интервалы. Этот факт означает, что рассматриваемая оцененная модель адекватна с 95 % вероятностью, а значит, она может быть использована для изучения объекта оригинала, а именно: прогноза значений средних оптовых цен на бензин АИ-95 операторов Московского региона по полной себестоимости добычи (поставки) тонны нефти.
Полученная модель может быть использована заинтересованными лицами, такими как, например, компании, государство, предприятия для реализации своих коммерческих целей по конкретным субъектам РФ.

