В наше время большинство людей умножают числа либо классическими методами, либо с помощью калькулятора, не предполагая о существовании каких-либо других методов умножения. В данной научной работе рассматриваются способы классического умножения и один из методов нетрадиционного умножения чисел.
Рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе.
Первый способ – раскладка на десятки и единицы [1, 2]. Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно сразу несколько чисел и при этом параллельно производить арифметические действия.
Например:
86*37 = (80+6)*(30+7) = 80*30 + 80*7 +
+ 6*7 + 6*30 = 2400 + 560 + 42 + 180 = 3182.
Таким образом, решая пример таким способом, мы совершаем три действия:
1) Разбили множители на десятки и единицы;
2) Перемножили числа, раскрыв скобки, учитывая знаки;
3) Получившиеся значения суммировали и получили ответ.
Проще такие примеры решаются в три действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
1) 80*30 = 2400 – запоминаем;
2) 80*7 + 6*30 = 740 – запоминаем;
3) (2400 + 740) + 6*7 = 3182 – ответ.
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме.
Второй способ – арифметические подгонки [2]. Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ.
Например:
49*49 решается так: (49*100)/2-49.
Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
И, наконец, рассмотрим один из нетрадиционных для нашей российской школы методов умножения- японский.
Археологами в Японии была найдена деревянная табличка с фрагментом таблицы умножения, которая предположительно была изготовлена в VIII веке. Учёные полагают, что подобные таблицы использовались японскими императорскими чиновниками, которым было необходимо осваивать разные науки, в том числе и арифметику. Обнаруженная табличка – самая древняя из всех найденных в Японии ранее. Интересно, что иероглифы, которыми записаны цифры, по стилю графического начертания очень похожи на те, которые использовались как официальное письмо во времена китайской династии Тан VII-X века. Исходя из этого, ученые предположили, что таблица была скопирована из китайского учебника арифметики того времени, то есть вся японская таблица умножения была заимствована из Китая.
Именно к своим соседям в Китай ездили высокопоставленные японцы каждый год, чтобы перенять у них разные науки, такие как арифметику. Древняя китайская таблица умножения была не из простых, так как включала в себя умножение двузначных чисел друг на друга. Вряд ли все японские чиновники могли выучить такую таблицу наизусть, поэтому и носили с собой на работу что-то вроде шпаргалок, фрагмент одной из которых и представляет собой найденная археологами в Японии табличка.
Итак, японская таблица умножения была заимствована у китайцев, которые, согласно некоторым гипотезам, и были одними из создателей первой арифметической системы, о чем свидетельствуют археологические находки, содержащие фрагменты таблицы умножения, возраст которых ученые оценили в 2700-3000 лет.
Японское умножение помогает не только быстро и эффективно умножать двухзначные и трехзначные числа друг на друга без калькулятора, но и развивает эрудицию. Согласитесь, не каждый сможет похвастаться тем, что на практике владеет древнейшим китайским методом умножения, который актуален и прекрасно работает и в современном мире.
Возьмем пример: 53*37=?
При умножении таким способом необходимо знать, что линии левого числа, в нашем случае (53) – рисуются горизонтально (сверху – вниз), а линии правого числа (37) – рисуются вертикально (слева – направо). Каждая цифра означает количество линий. Приступим к рассмотрению этого метода.
1. 53*37
Первая цифра в числе (53) цифра (5), следовательно, рисуем 5 линий (рис. 1).

Рис. 1. 5 линий
2. 53*37
Вторая цифра в числе (53) цифра (3), это значит, рисуем 3 линии, но они будут располагаться уже ниже ранее нарисованных линий (рис. 2).

Рис. 2. 3 линии
3. 53*37
Первая цифра в числе (37) цифра (3), рисуем 3 линии, но они будут располагаться уже вертикально
4. 53*37
Вторая цифра в числе (37) цифра (7), рисуем 7 линий, они будут также вертикально расположены и правее (рис. 3).
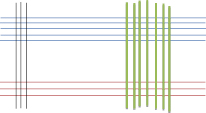
Рис. 3. Изображение числа 37вертикальными линиями
5. Выделяем зоны точек пересечения линий и записываем количество этих точек напротив каждой зоны (рис. 4).

9 + 35 = 44
Рис. 4. Выделение зон и подсчет пересечений
6. Запишем числа, которые у нас получились: 15, 44, 21.
Если же получились числа с десятками, то делам перенос десятков следующим образом (рис. 5):
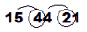
Рис. 5. Перенос десятков
То есть 15 + 4 = 19, 4 + 2 = 6.
Запишем эти числа уже с учетом изменений и получим ответ: 1961.
Проведём сравнительный анализ классических и нетрадиционного метода умножения. Классические методы требуют знание таблицы умножения, постоянное запоминание чисел, чтобы в дальнейшем прийти к правильному ответу. Нетрадиционный метод более легкий, этим методом можно пользоваться, не зная таблицы умножения и без помощи калькулятора, при этом при себе нужно иметь только пишущий предмет и объект, на котором будет проходить визуальное представление. Но, при расчетах больших чисел возникнет проблема: очень много линий.
Результаты исследования используются в качестве контента информационно-образовательной среды кафедры ОНД АМТИ [3-7].

