В информационной образовательной среде (ИОС) кафедры могут быть размещены не только интерактивные обучающие документы, но и электронные учебные пособия, обучающие программы и т.п. ([1], [3]). Рассмотрим ситуацию, в которой нет возможности использовать в чистом виде интерактивные обучающие документы. В частности, это может быть так называемый «гибридный документ», в котором могут быть ссылки на соответствующие электронные учебные пособия, обучающие программы и др. ([1]).
Возникает подобная ситуация, к примеру, во время изучения множеств на плоскости. Числовые множества на R×R являются обобщением числовых множеств на R. При этом средствами офисных программ можно изобразить не все множества, да и подготовка некоторых изображений множеств занимает слишком много времени и требует определённых навыков работы с графикой и псевдографикой. Всё это может только отвлечь обучающегося от непосредственного изучения учебного материала. Рассмотрим часть документа.
Представим с помощью объяснительно-иллюстративного метода круг (рис. 1).
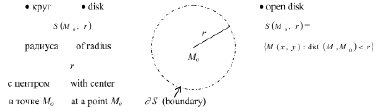
Рис. 1. График множества – открытый круг
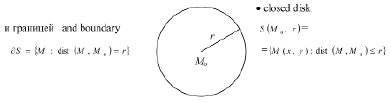
Рис. 2. График множества – замкнутый круг
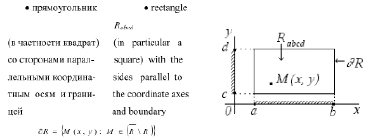
Рис. 3. График множества – прямоугольник
При этом R и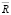 
имеют следующий смысл (рис. 4).
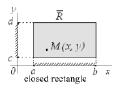
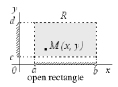
Рис. 4. График множества – замкнутый и незамкнутый прямоугольники
В настоящей статье представлены фрагменты из диссертации одного из авторов. Один из фрагментов (рис. 1) приведённый в ([5]) содержит русский и английский текст – как современные учебные пособия. На рис. 2 продолжение определения.
Рассмотрим определение множества – прямоугольник на плоскости.
Указанные выше формулы (ниже рис. 4) практически невозможно набрать в Microsoft Equation, поэтому необходимо использовать некоторые готовые шаблоны или рисунки, которые затем встраиваются в обучающую программу.
В указанных выше двух определениях фигур используется теоретико-множественный подход к фигуре, как множеству точек. Рассмотрим укрупнённую дидактическую единицу (УДЕ), в которой прямую задачу предложил преподаватель, а обратную составили и решили сами обучающиеся.
Прямая задача (Direct problem) № 1.
I.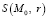 
: 
.
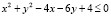II. Mo, r.
III.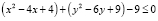 
.
.
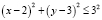Mo(2, 3), r = 3 (рис. 5). >
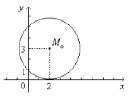
Рис. 5. График множества – круг
Обратная задача (Inverse problem) № 2.
I.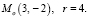 
(рис. 6)
II.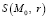 
.
III.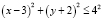 
.
.
. >
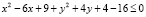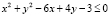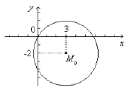
Рис. 6. Иллюстрация условия задачи
После выполнения ещё целого ряда УДЕ на множество круг, замкнутый или открытый, обучающимся предлагается УДЕ на произведение множеств – прямоугольник. Приведённая ниже УДЕ имеет все признаки обобщённой укрупнённой дидактической единицы, т.к. в ней применяется достаточно много математических операций изучаемой темы.
Приведём пример условия такой УДЕ (прямой и обратной).
Прямая задача (Direct problem) № 3.
I. Fig b =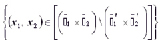 
.
when (где) ●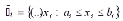 
,
● 
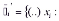
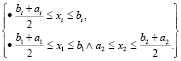
II. Геометрическую интерпретацию Fig b.
После решения обучающиеся приступают к составлению и решению обратной задачи.
Обратная задача (Inverse problem) № 4.
I.
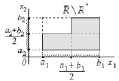
Рис. 7. Иллюстрация условия задачи
II. Теоретико-множественное представление Fig b.
Рамки статьи не позволяют в полной мере представить все стороны теоретико-множественного подхода к графикам числового множества, как множеству точек.
Приведённые в статье теоретико-множественные определения и иллюстрации некоторых плоских фигур, решение УДЕ и приведённые условия УДЕ на прямоугольник, мотивируют обучающихся осваивать учебный материал в активной и интерактивной формах ([4]). По результатам изучения темы авторами была подготовлена структура обучающей программы, необходимые шаблоны и отдельные фрагменты. Ведётся предварительная сборка обучающей программы.