Рассматриваемые методы при оценке рассеивающих свойств объектов можно условным образом разбить по трем классам. Первый из них связан с асимптотическими методами. Среди них применяют геометрическую оптику, физическую оптику, геометрическую теорию дифракции [1, 7]. Ко второму классу относятся строгие методы – интегральных преобразований, методы, базирующиеся на интегральных уравнениях. И еще, к третьему классу относят комбинированные методы.
В качестве примера подобных подходов можно указать метод стационарного функционала Ю. Швингера, различные гибридные способы, в которых сочетают целую совокупность методов и др.
Выделяют три характерных области, в пределах которых могут быть размеры рассеивателей L: квазистатическая (по-другому ее называют релеевской), тогда L/( l lt; lt; 1; резонансная, тогда L/l ( l~ 1; квазиоптическая, тогда L/( l gt; gt; 1 ((l– является длиной радиоволны).
Для квазистатической области решения задач могут получиться на базе решений волновых уравнений (уравнений Гельмгольца), но решения аналитическим способом можно достичь не всегда и необходимо использовать численное решение.
Для резонансной области (ее рассматривают как трудную в исследовательских задачах) во многих случаях прибегают к методу разделения переменных или методу интегральных уравнений.
Для квазиоптической области могут быть использованы два вида способов: лучевые и волноводные. Лучевые методы, в основном могут быть представлены геометрической оптикой и ее уточнениями.
Множество экспериментальных методов, связанных с определением характеристик вторичного излучения может быть подразделено по методам: проведение натурных измерений; использование масштабных электродинамических моделирований; масштабных акустических моделирований.
В методах натурных измерений выделяют два подхода: динамические и статические измерения.
Снятие динамических характеристики происходит для процессов реальных полетов, при этом необходимо применять соответствующие приборы.
Снятие статических характеристик происходит [2, 5] на испытательных полигонах. Идет закрепление объектов на необходимых высотах по отношению к земной поверхности на основе тросов или применяются покрытые слабоотражающими материалами колонны, их [4, 6] и поворотные устройства соединяют.
Реализацию метода масштабного электродинамического моделирования осуществляют при помощи полигонных установок, которые являются аналогичными применяемым при процессах натурного статического моделирования или для безэховых камерах.
В методе гидроакустического моделирования используют аналогию акустических и электромагнитных волновых процессов в изотропных средах.
Увеличивающиеся возможности в области радиолокационных сенсоров и растущие значения пропускной способности каналов беспроводной связи определяют непрерывный рост объемов данных по изображениям, которые передаются в радиолокационные центры обработки. При таких условиях актуальной может считаться автоматизация, тех основных операций по анализу и осуществления интерпретации радиолокационных изображений (РЛИ), их на настоящее время выполняют квалифицированные эксперты.
Объект, представленный совокупностью независимых отражателей, расположен на опорно-поворотном устройстве (рис. 1). Антенна А располагается в дальней зоне, создает поле облучения и осуществляет прием рассеянного объектом поля в наборе k = 0...Nk – 1 точек. Задачей является определение амплитудно-фазового распределения (АФР) поля вторичного излучения объекта в рабочей зоне D по массиву Ek зарегистрированных отсчетов диаграммы обратного рассеяния (ДОР).
При использовании радиоголографического подхода, с учетом изменения структуры поля облучения в процессе измерений, расчет РЛИ можно провести следующим образом [8, 9]:
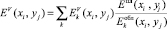, (1)
,
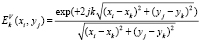где xi, yj – точки изображения, i = 0...Ni – 1, j = 0...Nj – 1,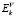 
– АФР в области D, восстанавливаемое с k-й точки наблюдения, 
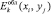– АФР антенны при расположении антенны в k-й точке наблюдения, Eпл – АФР плоского поля, распространяющегося в направлении j = 0, 
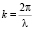, l – длина волны, xk = Rcosjk, yk = Rsinjk – координаты точки наблюдения, R – расстояние до объекта, удовлетворяющее условию дальней зоны, jk – угол наблюдения.
После подстановок (1) принимает вид
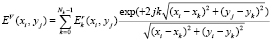. (2)
Выражение (2) представляет основу для синтеза первого алгоритма восстановления РЛИ.
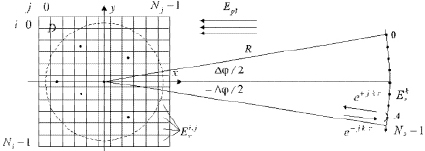
Рис. 1. Схема рассеяния электромагнитных волн на объекте
Второй подход к получению РЛИ заключается в рассмотрении задачи восстановления как обратной.
Отсчеты зарегистрированного массива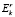 
, k = 0.. Nk – 1, представляют «смазанный» образ РЛИ. Элементы оператора искажений А находятся из вида выражения, описывающего прямой процесс формирования поля вторичного излучения объекта.
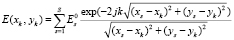, (3)
где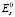 
– поле вторичного излучения (неизвестное) в рабочей зоне радиолокационного измерительного комплекса, s – индекс, принимающий значение 0...S – 1, S = Ni-1Nj-1
В последнем выражении
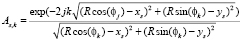, (4)
– элементы обратного оператора, где k = 0…K, i = 0..Ni – 1.
Строится обобщенная матрица системы линейных уравнений
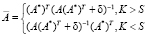, (5)
где d – параметр регуляризации. Параметр регуляризации d = 10-10.
Далее определяется восстанавливаемое изображение
J =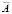 
Es1, (6)
где Es1 = Es(Ek, yk).
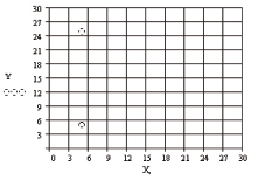
Рис. 2. Расположение локальных отражателей
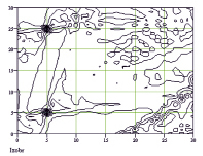
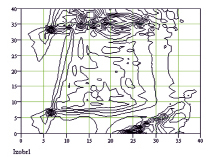
Рис. 3. Результаты восстановления изображения на основе первого (а) и второго (б) алгоритмов
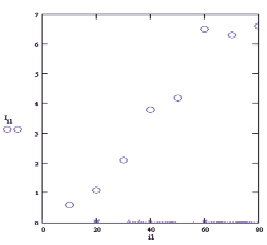
Рис. 4. Результаты восстановления максимума второго источника
С использованием алгоритмов (1)-(2) и (3)-(6) проводилась оценка разрешающей способности локальных отражателей [3, 10] в виде точечного источника. Расстояние до локального отражателя составляло R = 500l, сканирование проводилось в плоскости X, Y =1l..30l. Видно (рис. 4), что значение максимума второго источника зависит практически линейно от сектора углов наблюдения.