Во время изучения сходящихся последовательностей обучающиеся подготавливают после соответствующей лекции по заданию преподавателя интерактивные обучающие документы ([1]). Для качественного изучения учебного материала возникает необходимость в самостоятельном изучении отдельных вопросов темы, не изученных на лекции ([2]).
Для самостоятельного изучения более предпочтительно использование технологии укрупнённых дидактических единиц (УДЕ), в частности обобщённых укрупнённых дидактических единиц (ОУДЕ) ([4], [5]), которые включают в себя большинство математических операций, изучаемых в разделе или теме.
Вся история применения УДЕ убеждает, что во время занятия (будь то лекционное или практическое) наряду с традиционными заданиями необходимо использовать «многокомпонентное задание, образующееся из нескольких логически разнородных, но психологически» ([7], стр.19) собранных в единое целое, состоящих в решении стандартной задачи, составлении и решении обратной задачи, аналогичной для прямой и обратной, обобщённой по некоторым параметрам исходной (стандартной).
Решение приведённого далее примера основывается на ряде теорем, касающихся сходящихся последовательностей – имеет только один предел, ограничена; сумма (разность, произведение, частное, при условии, что предел знаменателя не равен нулю) двух сходящихся последовательностей – сходящаяся последовательность, при этом предел её равен сумме (разности, произведению, частному) пределов. Необходимо отметить, что во время проведения литературного обзора подобных задач и их решений не имеется ни в одном из источников. Тем самым данное исследование имеет научную новизну и, как следствие, практическую значимость для процесса обучения.
Рассмотрим следующую ОУДЕ.
ОУДЕ № 1. Прямая задача.
I. 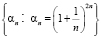 ,
, 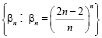 .
.
II. 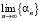 ,
, 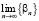 ,
, 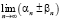 ,
, 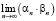 ,
, 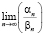 ,
, 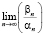 .
.
III. 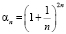 ⇒
⇒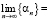
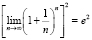 ,
,
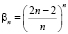 =
= 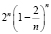 ⇒
⇒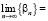
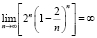 .
.
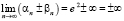 ;
; 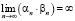 ;
; 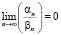 ;
; 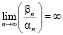 .
.
Рассмотрим следующую задачу, которая является обратной задачей по сути, но не по содержанию.
Обратная задача
I. 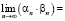
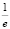 ,
, 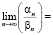
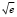 .
.
II. 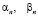 .
.
III. 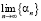
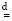 ⇒,
⇒, 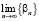
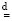 ⇒
⇒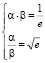 ,
, 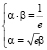 ,
, 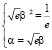 ,
, 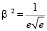 ,
,
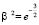 ,
, 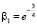 , ⇒
, ⇒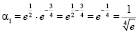 ⇒
⇒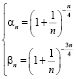 ,
,
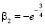 , ⇒
, ⇒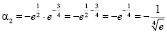 ⇒
⇒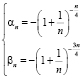 .
.
Проанализировав приведённую выше ОУДЕ, обучающиеся самостоятельно приступают к составлению и решению аналогичных задач. Приведём некоторые результаты их опытов. Напомним, что решить ОУДЕ – значит решить прямую задачу, составить обратную и решить также её.
1. Даны последовательности: 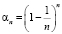 ,
, 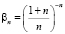 . Вычислить
. Вычислить 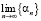 ,
, 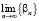 ,
, 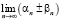 ,
, 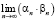 ,
, 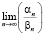 ,
, 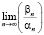 . Решить ОУДЕ.
. Решить ОУДЕ.
2. Даны значения: 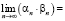
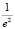 ,
, 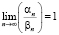 . Записать представление
. Записать представление 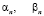 . Решить ОУДЕ.
. Решить ОУДЕ.
3. Даны последовательности: 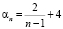 ,
, 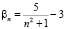 . Вычислить
. Вычислить 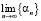 ,
, 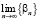 ,
, 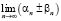 ,
, 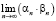 ,
, 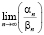 ,
, 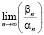 . Решить ОУДЕ.
. Решить ОУДЕ.
4. Даны значения: 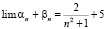 и
и 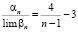 . Записать представление
. Записать представление 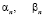 . Решить ОУДЕ.
. Решить ОУДЕ.
Рассмотрим ещё несколько примеров, для которых легко составить обратные задачи, которые нужно затем решить.
УДЕ № 2.
I. 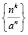 – последовательность, a gt; 1.
– последовательность, a gt; 1.
II. Доказать, что заданная последовательность бесконечно малая.
III. Пусть некоторое число 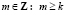 , тогда
, тогда
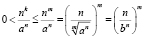 ,
,
где 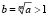 .
.
Оценим полученный результат:
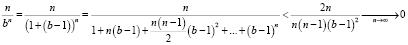
Следовательно,
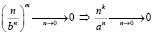 .
.
По определению такая последовательность бесконечно малая ч.т.д.
УДЕ № 3.
I. 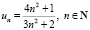 – последовательность.
– последовательность.
II. Доказать, что 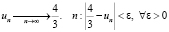 .
.
III. 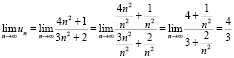 .
.
Выберем число 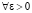 , рассмотрим
, рассмотрим
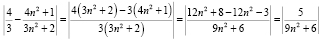 ,
,
т.к. 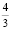 – предел, то должно (по определению) выполняться следующее неравенство
– предел, то должно (по определению) выполняться следующее неравенство
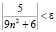 .
.
Находя обратные величины, получаем:
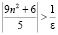
и, тогда
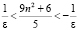 ,
,
при этом правая часть двойного неравенства не может иметь места (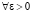 ). Следовательно,
). Следовательно,
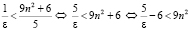
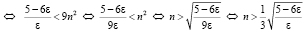 .
.
Результат надо интерпретировать так, что
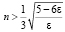 при
при 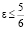 и
и 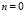 при
при 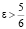 . Это и является ответом.
. Это и является ответом.
УДЕ № 4.
I. Последовательности 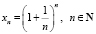 и
и 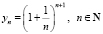 .
.
II. Доказать, что 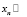 и ограничена сверху,
и ограничена сверху, 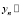 и ограничена снизу, и имеют общий предел:
и ограничена снизу, и имеют общий предел: 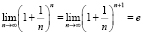 .
.
III. Отношения 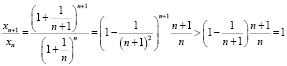
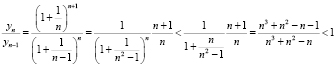 .
.
Для их вывода использовалось простое неравенство:
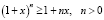 .
.
Из полученных двух отношений следует, что 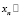 ,
, 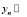 , а также
, а также
xn lt; yn.
Вычислим разность
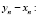
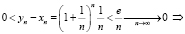
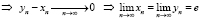
(полученное равенство называется вторым замечательным пределом).
Решения прямых задач со второй по четвёртую вносятся в интерактивный обучающий документ. Для каждой из них составляется обратная, которые также вводятся в документ.
Наиболее значимым с точки зрения методики является самостоятельность в составлении и решении аналогичных ОУДЕ, включение их в обучающие интерактивные документы доступные всем студентам группы для совместного анализа и обсуждения ([3], [6]), по результатам которых делается обобщённый вывод. В самой структуре УДЕ и ОУДЕ заложена успешность усвоения учебного материала. Занятие, построенное таким образом, проходит в активной и интерактивной форме и, несомненно, мотивирует студентов заниматься учебно-исследовательской, а далее и научно-исследовательской работой.

