Статистическая обработка данных применяется во многих областях науки и общества – это и технические науки, и экономика, социология, менеджмент и др. Будущие специалисты должны уметь выявлять взаимосвязи и закономерности в производственных и экспериментальных данных. В информационной образовательной среде (ИОС) кафедры должны размещаться не только общенаучные учебные материалы, но и имеющие отношение к избранной профессии, в частности в области электроэнергетики и электротехники. Авторы предлагают в настоящей статье фрагмент интерактивного обучающего документа по обработке экспериментальных данных, в котором моделируется вполне вероятная ситуация на производстве в ходе испытания некоторого электротехнического устройства ([2–4]).
Во время изучения вопросов приближённых вычислений по дисциплине «высшая математика» и численных методов дисциплины «специальные главы математики» нами изучаются способы и методы обработки экспериментальных данных. Мы подготовили документ, в котором раскрывается теоретическая и практическая стороны задачи ([1]).
В начале этого документа приводится схема некоторого устройства с входным х и выходным у сигналами. При этом неизвестно, какой функциональной зависимостью связаны указанные величины. Ставится задача получить эту функциональную зависимость y = φ(x), используя экспериментальные данные, полученные в ходе эксперимента.
Экспериментальные данные получаем: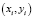 
, где i = 1..n. Из теории известно, что через точки можно провести кривую, задаваемую многочленом (n –1)-й степени, называемым интерполяционным. Интерполяция может неверно отображать ситуацию из-за случайных ошибок измерения и влияния на измерения значений yi помех и шумов в устройстве.
Задача получения кривой (называемой аппроксимирующей) мало зависящей от случайных ошибок есть сглаживание (аппроксимация) экспериментальной зависимости.
Решение задачи проводим методом наименьших квадратов. Экспериментальные точки наносятся на координатную плоскость, приблизительно оценивается, к какому классу функций относится искомая функция. Будет ли это линейная функция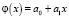 
, квадратичная 
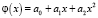и вообще, функция вида: 
.
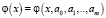В последней функции неизвестные параметры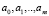 
определим с помощью минимизации вспомогательной функции
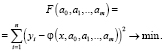
Обозначим величину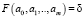 
, которую назывём суммарной невязкой.
Из курса высшей математики известно, что необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных этой функции (невязки). Находим частные производные невязки (система из m равенств).
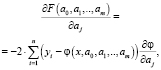
где j = 0, 1,..,m.
Приравниваем найденные частные производные нулю.
,
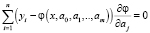где j = 0, 1,..,m.
Решая систему уравнений, находим неизвестные параметры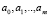 
, что полностью определяет искомую функцию.
Приведённое выше – очень краткое изложение теоретического материала использования метода наименьших квадратов для аппроксимации экспериментальных данных.
Рассмотрим задачу: получить функцию аппроксимирующую экспериментальную зависимость. Задано семь пар значений вида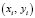 
. Запишем базу данных экспериментальных точек в математической среде MathCAD.
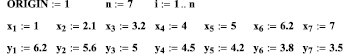
Значения переменных xi и yi заданы в виде двух векторов с одинаковым количеством элементов (по семь), над которыми производятся вычисления.
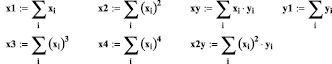
Именно по этим формулам и происходит расчёт неизвестных коэффициентов вспомогательной функции с использованием вычислительного блока Given … Find.
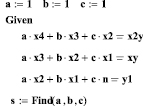
Т.к. в переменную s записан вектор, то увидим его содержимое и используем для получения аппроксимирующей функции.
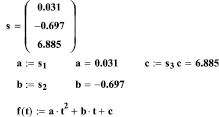
Выведем график на экран компьютера (рисунок).
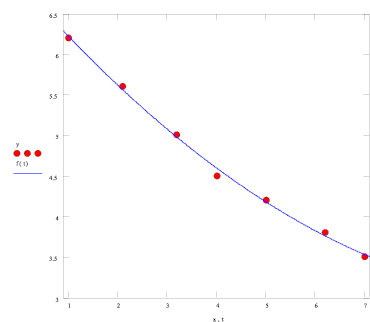
График аппроксимирующей кривой по экспериментальным точкам
И становится очевидным, что аппроксимация квадратичной функцией очень хорошо описывает экспериментальные точки. Тем более что невязка достаточно малая.
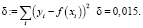
Составленный интерактивный обучающий документ позволяет в активной и интерактивной формах изучать представленный учебный материал ([5]). При этом у студента может создаться впечатление, что совсем не обязательно вникать в доказательство вполне определённых математических формул, некоторых теоретических фактов. Но ведь математическое мышление не может быть заменено программой. Для того, чтобы студент мог подготовить соответствующий интерактивный обучающий документ, ему придётся предварительно изучить учебный материал, пропустить его через себя. Тем самым освоение учебного материала проходит в активной и интерактивной формах. Все изученные понятия, формулы и зависимости при таком обучении становятся «достоянием» долговременной памяти обучающихся, т.к. будущему специалисту нужно чётко представлять, почему применяется та или иная формула. Это очень хорошо видно из представленного интерактивного обучающего документа.