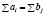Экономическая грамотность человека зависит от того, насколько, он владеет математическими знаниями, и как он может их применять при решении сложных экономических проблем. Необходимость изучения экономических задач осуществляется, с помощью различных методов: математической статистики, теории вероятностей, моделирования, методов оптимизации, а также линейное программирование [1].
Линейное программирование является ветвью математического программирования – это раздел математики, разрабатывающий различные методы решения экстремальных задач.
Наиболее распространенная задача линейного программирования является транспортная задача — задача о поиске экономичного плана перевозок однородного продукта из пунктов производства в пункты потребления. [2]
Типы транспортных задач
1. Транспортная задача по критерию стоимости перевозок.
2. Транспортная задача по критерию времени.
3. Транспортная задача на определение кратчайшего из расстояний по заданной сети дорог и задачи на введение максимального потока в цепи.
Общая постановка задачи. В трех пунктах отправления A1, A2, A3 сосредоточен груз в количествах a1, a2, a3. Этот груз следует доставить в каждый из четырех пунктов назначения B1, B2, B3, B4 в количестве b1, b2, b3, b4 соответсвенно. Стоимость перевозок единицы груза из i-го пункта отправления в j-ый пункт назначения равна cij. Определить план перевоза такой, чтобы его стоимость была наименьшей (таблица).
|
Вj Ai |
B1 |
B2 |
B3 |
B4 |
Запасы |
|
A1 |
c11x11 |
c12x12 |
c13x13 |
c14x14 |
a1 |
|
A2 |
c21x21 |
c22x22 |
c23x23 |
c24x24 |
a2 |
|
A3 |
c31x31 |
c32x32 |
c33x33 |
c34x34 |
a3 |
|
Потребн. |
b1 |
b2 |
b3 |
b4 |
|
Модель задачи
xij – количество груза, перевозимого из Ai в Вj.
Если равенство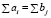 
выполняется, то это так называемая закрытая модель транспортной задами, если не выполняется, то модель открытая.
При решении задачи с открытой моделью вводят или ложный пункт отправления, или ложный пункт назначения с нулевыми тарифами.
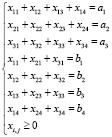
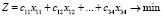
Если m – число пунктов отправления, а n – число пунктов назначения, то уравнений составлено m + n, а переменных – m∙n.
Можно показать, что одно из уравнений системы лишнее (оно является следствием остальных), его можно исключить из системы.
Таким образом, в общем случае т.з. система должна иметь m + n – 1 – уравнений с m∙n – переменными, причем эта система всегда разрешима относительно (m + n – 1) переменной.
О. План перевозок, обращающий в min суммарные транспортные издержки, называется оптимальным планом или оптимальным разрешением транспортной задачи.
Построение начального плана перевозок
Алгоритм заполнения выбранной клетки таблицы одинаков для всех методов составления опорного плана грузоперевозки.
Возможны два случая:
a) min (a1, b1) = a1; x11 = a1, тогда x12 = x13 = x14 = 0.
Вместо b1 останется (b1 – a1).
б) min (a1, b1) = b1; x11 = b1 x21 = x31 = 0. Вместо a1 остается (a1 – b1).
Все методы построения опорного плана перевозки отличаются друг от друга только способом выбора клетки заполнения.
Метод северо-западного угла
Алгоритм, по которому элементы xij плана определяют, начиная с левого верхнего угла таблицы, называют методом северо-западного угла (тарифы не учитываются).
Ненулевые перевозки xij принято называть базисными, а нулевые – свободными.
Начальный план перевозок, составленный по методу северо-западного угла, является допустимым.
xij ≥ 0.
План перевозок, в которых число базисных неизвестных равно m + n – 1 называется невырожденным. Если меньше этого числа, то план вырожденный и значит нужно ввести перевозку с нулевым тарифом.
Метод минимального элемента
для составления первоначального
плана перевозок
1. В плане заполняется клетка, которая соответствует min тарифу.
2. Затем заполняется клетка с min тарифом среди оставшихся и т.д.
3. Если на некотором шаге возникнет ситуация, когда несколько min элементов одинаковых, то min тот, у которого меньше индекс i.
4. В общем случае, нельзя сказать, какой план перевозок ближе к оптимальному. Чаще оказывается ближе метод min элемента.
Метод аппроксимации Фогеля
1. Условие задачи записывают в виде таблицы со свободными нулевыми строкой и столбцом.
2. Для их заполнения вычисляют разности αi по строке и βj по столбцу между min элементом тарифа и следующим по величине элементом. Если i-строка (или j-столбец) содержит более одного min элемента, то αi = 0 (βj = 0).
3. После заполнения строки и столбца разностей выбирают наибольшую м начинают заполнять таблицу с клетки, ей соответствующей. Возможны два случая:
• Если имеется лишь одна наибольшая разность, начинаем заполнять клетку ей соответствующую. Затем эти разности исправляются и строят новые.
• Если несколько равных между собой наибольших разностей, то начинают заполнять ту клетку, у которой наименьший элемент в столбце является наименьшим и в строке.
Метод потенциалов решения транспортных задач
Произвольная совокупность клеток с перевозками называется набором.
О. Набором клеток (1;1), (1;3), (3;3), (3;1) называют цепью, так что каждая пара соседних клеток цепи расположена либо в одной строке, либо в одном столбце таблицы (причем никакие три клетки цепи не лежат ни в одной строке или в одном столбце).
О. Если последняя клетка лежит в одной строке (столбце) с первой, то такая цепь называется замкнутой или циклом.
Если цепь незамкнута, то план перевозок называется ациклическим. Первоначальный план всегда ациклический.
Теорема. Для того, чтобы план перевозок был оптимальный, необходимо и достаточно, чтобы ему соответствовала такая система из m + n чисел таких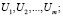 
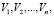для которой выполняются условия:
1. 
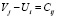– для всех клеток xij плана перевозок 
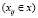заполненных.
2. 
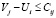– для всех клеток, не входящих в план перевозок 
.
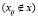Числа Ui и Vj называются потенциалами соответствующих пунктов отправления и назначения.
Одной из видов транспортной задачи является классическая. Это задача оптимального плана перевозок однородного продукта в однородные пункты потребления на однородных транспортных средствах. [3]
Транспортная задача является особой формой поиска оптимального плана перевозок груза с минимальными затратами. С помощью транспортной задачи можно найти оптимальный план перевозки грузов, затрачивая при этом, минимальное количество затрат. [4]
Цель транспортной задачи – обеспечить доставку продукции потребителю в нужное время и место при минимальной стоимости трудовых, материальных и финансовых ресурсов. Цель считается достигнута, когда выполняются следующие условия:
– необходимый товар;
– достойное качество;
– необходимое количество;
– нужное время;
– нужное место;
– минимальные затраты.
Приведем пример транспортной задачи:
Пусть некоторый однородный груз сосредоточен у mпоставщиков в объемах. Это груз нужно доставить n потребителям в объемах. Известны (i = l, 2,..., m, j = l, 2,..., n) – стоимость единицы груза от каждого i-roпоставщика каждому j-му потребителю. Составим план транспортировки груза, при котором запасы всех потребителей полностью удовлетворены, и общая стоимость перевозки грузов минимальна. Первичные данные транспортной задачи, как правило, записываются в виде таблице или векторов фонда поставщиков, потребительского спроси и матрицы стоимостей. Неизвестные параметры транспортной задачи обозначим (i = l, 2,.., m, j = l, 2,.., n)-v – объемы перевозок от каждого i-ro поставщика каждому j-му потребителю.
Существует два типа моделей транспортной задачи: открытый и закрытый.
Открытая модель задачи предполагает, наличие равенства между общими расходами поставщиков и общим расходам потребителям (задача с правильным балансом).
Если этого равенства нет, то модель этой задачи является открытой (задача с неправильным балансом).
Транспортная задача решается несколькими методами:
1. Метод «северо-западного угла». На каждом шаге построения изначального опорного плана таблица заполняется по диагонали, начиная с левой верхней клетки (северо-западный угол. При этом вычеркивается каждый столбец (строка), предполагая, что число этого столбца (строки) равно нулю.
2. Метод минимальной стоимости. При этом методе первой заполняется та клетка таблицы, имеющая наименьшее число. Если такая клетка не одна, то можно заполнить любую из них. Процесс распределения запасов длится до тех пор, пока все запасы не будут удовлетворены.
3. Метод Фогеля. В распределительной таблице по строкам и столбцам выделяется наибольшая разность между двумя наименьшими тарифами. В строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза дальше не учитываются. Далее на каждом этапе загружается только одна клетка. Как и в предыдущем методе, решение задачи происходит до удовлетворения всех потребностей.
Таким образом, можно сделать вывод, что решение транспортных задач, позволяет найти минимальные затраты на перевозку грузов, выбрать кратчайшей путь маршрута, снизить количество времени на доставку груза, а также сократить различные расходы, что приведет конкурентоспособности самого малого предприятия.