Теория вероятности и математическая статистика широко используется для решения различных задач во многих сферах жизни, особенно распространено использование этих разделов в экономических задачах для нахождения важных показателей, используя математическое моделирование, так как экспериментальные исследования невозможны или экономически нецелесообразны [2].
Одной из сфер в экономике, которая применяет различные методы теории вероятности и математической статистики является сфера страхования.Математические модели страхования применяются для описания деятельности обособленных страховых организаций, целью которых является продажа страхового обеспечения. В основном задачи, решаемые экономистами страховых компаний, являются комплексными, так как в условиях уже содержат рассчитанные элементы, связанные с теорией вероятности, обычно это результаты многолетних наблюдений и расчетов специалистов. Например, к таким элементам относят вероятность смерти в определенном возрасте или вероятность наступления другого страхового случая.
Для решения задач необходимо знать основы теории вероятностей и ряд формул, которые могут быть использованы при решении [1]. Рассмотрим некоторые теоретические аспекты, которые чаще всего будут применены в решениях задач ниже.
Используя формулыразделов теории вероятностей и математической статистики, страховая компания может рассчитать вероятность получения убытка или возможность превышения дохода от заданной фиксированной величины [5]. Рассмотрим соответствующую задачу.
Допустим что, вероятность смерти тридцатилетнего мужчины составляет 0,006. Страховая компания заключила 10 тыс. страховых договоров с мужчинами в возрасте до 30-ти лет. Согласно договорув случае смерти застрахованного лица в течениеближайшего года его ближайшим наследникам (по закону) выплачивается 100 тыс. руб. Стоимость заключения одного страхового полюсаравна 1200 руб. Найти вероятности следующих событий: а) компания потерпит убыток в конце года; б) доход страховой компании составит более 4 млн руб.
Пусть за год наступило k страховых случаев, тогда доход страховой компании составит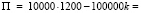 
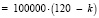руб.
Поэтому компания окажется в убытке (П < 0), если за год наступит более 120 страховых случаев (то есть от 121 до 10000 страховых случаев).
Доход страховой компании превысит 4 млн руб. (П > 4000000), если за год наступит менее 80 страховых случаев. Вероятность наступления страхового случая p = 0,006. Всего проводится n = 10000 испытаний. Поскольку число испытаний n велико, а произведение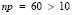 
, можно воспользоваться интегральной теоремой Муавра – Лапласа:
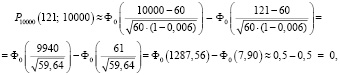
то есть страховая компания окажется в убытке с нулевой вероятностью;
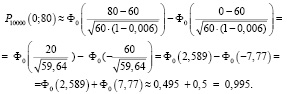
Значит, доход страховой компании превысит4000000 руб. с вероятностью, очень близкой к единице, то естьс высокой вероятностью в 99,5 %.
Также страховые компании могут рассчитать возможную прибыль, зная количество клиентов, вероятность наступления страхового случая и условия договора, которые предоставляются клиентам.
Предположим что, в страховой компании 10 тыс. клиентов. Страховой первоначальный взнос каждого клиента составляет 500 руб. Наступление страхового случая, согласно подсчетам и оценкам статистических экспертов, подвержено вероятности равной p = 0,005 страховая компания обязана выплатить клиенту страховую сумму размером 50 тыс. руб., в случае наступления страхового случая. Необходимо рассчитать потенциальную прибыль страховой компании с надежностью 95 %?
Размер прибыли компании составляет разность между суммарным взносом клиентов компании и суммой, которая будет выплачена n0 клиентам при наступлении страхового случая, то есть:
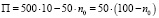тыс. руб.
Для определения n0 применим формулу Муавра-Лапласа:
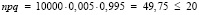, то есть требование выполнено [3].
По условию задачи:
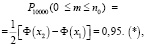
где m – число клиентов, которым будет выплачена страховая сумма;
,
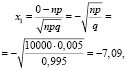
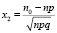откуда:
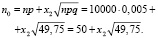
Из соотношения (*) получаем:
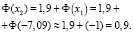
По таблице Ф(х2) = 0,9, при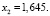 
Теперь: 
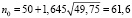и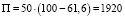 
тыс. руб. То естьс надежностью 0,95(95 %) ожидаемая прибыль составит 1,92 млн руб.
Многие расчеты полученные при помощи теории вероятности являются относительными, поэтому для их проверки используют показатели точности измерения. Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента) [4]. Некоторый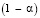 
– двусторонний доверительный интервал (XL, XU) для неизвестного параметра X есть интервал, обладающий тем свойством, что с вероятностью 1-α,он содержит истинное неизвестное значение параметра X. Величина 1-α характеризует неточность измерений, от неё зависит ширина доверительного интервала.
Принято в отчетах использовать 95 %-й доверительный интервал, согласно которому истинные значения принадлежат интервалу с вероятностью в 95 %.Страховая компания может предположить приблизительное количество потенциальных клиентов, путем статистической обработки социальных опросов, используя доверительный интервал определить истинный диапазон интересующих результатов.
Допустим, по предварительному опросу населения большого города, в которомучаствовало 900 жителей, застраховать свою жизнь (Х), по скидочным условиям страховой компании готовы 400 человек изопрошенных жителей. Необходимо найти 95 %-ый доверительный интервал, в котором находитсяистинный процент готовыхвоспользоваться данной услугой страховой компании.
Доверительный интервал для истинного процента (доли) p готовых застраховать свою жизнь Х, найдем по формуле:
,
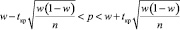где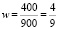 
– относительная частота (выборочная доля), а
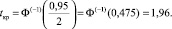
Подставляя исходные данные получим:
,
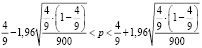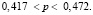
Это значит, что истинное значение готовых застраховать свою жизнь жителей (при прочих равных условиях) составляет от 41,7 % до 47,2 % от числа опрошенных значит, страховая компания имеет от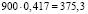 
до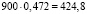 
потенциальных клиентов на предложенных условиях с 95 %-ной точностью.
Таким образом, хотелось бы отметить, что применение математических моделей с использованием методов теории вероятностей и математической статистики практически целесообразно при решении задач в сфере страхования и позволяет производить расчеты для нахождения экономически важных показателей для фирмы при планировании и прогнозировании.