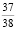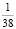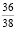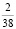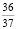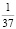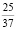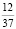Практически все естественные науки опираются на вероятностные методы. На самом деле, первые труды ученых-математиков, посвященные теории вероятности как науке, объектом исследования и изучения принимали выявление закономерности и возможности предвидения исхода азартных игр. Подобная наука не определяет точного результата игры, а лишь дает оценку возможностям и шансам игроков [2, 5].
Классической формулой вычисления вероятности и, соответственно, самым простым способом ее расчетаявляется формула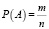 
. Возможно ее применение для оценки шансов выигрыша в лото. Допустим, всего номеров 90, а выбрать нужно 6, вероятность получения нужного нам номера равна 
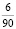или 1:15. Следовательно, вероятность полного совпадения шести номеров в имеющимся лотерейном билете: 
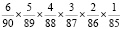или 1:622614630. Очевидна универсальность использования и применения данной формулы, что является бесспорным плюсом метода [8]. Однако, при подобном подсчете не учитываются шансы выиграть определенную сумму баллов или денежных средств, что является значительным минусом формулы [1, 9]. Следующим способом, возможным к применению, является определение математического ожидания азартной игры. Технология его использования заключается в сложении произведения вероятности данной комбинации и суммы очков, соответствующей позиции:
,
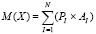где P – вероятность выигрыша/проигрыша, A – возможная сумма очков выигрыша/проигрыша, N – количество возможных исходов. Стоит отметить, что главный недостаток этого метода – сложность вычислений [4, 6]. Для примера можно использовать игру в кости. Допустим, выпадение 3 или 4 очков прибавляет нам 5 баллов, а выпадение 1,2,5,6 вычитает 3 балла из общего счета игры. Таким образом, математическое ожидание:
.
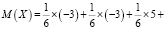
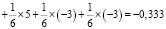Основываясь на отрицательном результате математического ожидания, можно сделать вывод о нецелесообразности и необоснованности игры. В случае увеличения выигрыша на 1 балл:
.
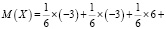
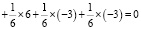Очевидно, в данном случае растут шансы на победу. Теперь попробуем уменьшить проигрыш на 1 балл. В этом случае:
.
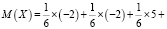
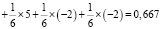Сейчас наши шансы на победу значительно возросли. Следовательно, игра на таких условиях более приемлема и выгодна из вышеперечисленных трех вариантов.
Так, рассмотрим более детально практическое применение метода математического ожидания. Наибольшую популярность и распространенность имеют рулетка и игровой автомат. На подобных азартных играх остановимся поподробнее. Самой первой из ныне существующих азартных игр является рулетка. Она впервые появилась в 1765 году во Франции. Наибольшую известность получили американская и европейская ее разновидности. Возможно, это связано с большим количеством ставок, которые могут произвести игроки. В американской рулетке 38 секторов и : прямая ставка – ставка на одно число. В случае победы оплачивается 35:1, т.е при условной ставке в 1 единицу и ее выигрыша, вы получаете 35 условных единиц, или проигрываете сумму в пределах вашей ставки. Далее ставка на 2 смежных числа и возможный выигрыш 17:1, на 3 – 11:1, на 4 числа, образующие квадрат на столе рулетки, – 8:1, на 5 чисел (0,00,1,2,3) – 6:1, если выпадет одно из вышеуказанных чисел, на 6 – 5:1, на 12 чисел возможна ставка несколькими способами, но несмотря на вариации, ставка оплачивается в соотношении 2:1 и на 18 чисел также несколько версий и оплата 1:1. Для того, чтобы понять, какая из модификаций наиболее выгодна для игрока, надо определить математическое ожидание для каждого случая по представленному образцу.
Пример 1: Рассчитать сумму возможного выигрыша для единственной ставки на одно число, принимая X за ее величину.
Решение:
|
X |
-1 |
35 |
|
P(X) |
|
|
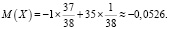
Ответ: данные условия являются несправедливыми, так как математическое ожидание меньше 0.
Пример 2: Рассчитать сумму возможного выигрыша для разовой ставки на два числа, принимая Xза ее величину.
Решение:
|
X |
-1 |
17 |
|
P(X) |
|
|
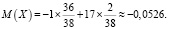
Ответ: данные условия являются несправедливыми, так как математическое ожидание меньше 0.
Проведя практическое исследование до конца, можно убедиться в том, что американская рулетка не предоставляет высоких шансов на выигрыш и является несправедливой игрой. Это доказывается равным во всех случаях математическим ожиданием.
Подобным образом разберемся с вероятностью победы в европейской рулетке или рулетке Монте-Карло. Итак, определим математическое ожидание при различных единичных ставках игрока.
Пример 3: Рассчитать сумму возможного выигрыша для единственной ставки на одно число, принимая X за ее величину.
Решение:
|
X |
-1 |
35 |
|
P(X) |
|
|
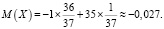
Ответ: данные условия являются несправедливыми, так как математическое ожидание меньше 0.
Пример 4: Рассчитать сумму возможного выигрыша для единственной ставки на дюжину (12 чисел), принимая X за ее величину.
|
X |
-1 |
2 |
|
P(X) |
|
|
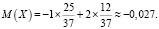
Ответ: данные условия являются несправедливыми, так как математическое ожидание меньше 0.
Следовательно, условия европейской рулетки не выгодны для игрока и также являются несправедливы. Применив методику решения в предыдущих двух примерах для дальнейшей проверки выводы, можно убедиться в объективности результатов и одинаковом во всех случаях математическим ожиданием равным -0,027.
Таким образом, стоит заключить, что в основе правил рулетки лежит следующий принцип: повышение вероятности определенного события уменьшает его ставку, но сохраняет неизменным математическое ожидание.
Следующей распространенной азартной игрой является игровой автомат. Приняв следующие правила игры, можно убедиться в справедливости или несправедливости предоставленного шанса разбогатеть. Стоимость участия в игре 5 денежных единиц. Величина выигрыша зависит от вариаций трех выпавших цифр и чтобы ее определить, следует умножить цену участия на соответствующее табличному значению цифр на игровом экране количеству монет. Учитывая, что возможность выпадения любой из цифр равновероятна, можно рассчитать шанс:
– выпадения трех одинаковых цифр
;
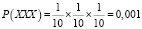– выпадения двух одинаковых цифр, а именно 7 и 0
.
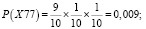
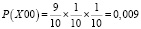– выпадения одной цифры по схеме XX0 и XX7 с учетом того, что второй цифрой не будет стоять 0 и 7 соответственно
.
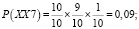
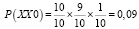По аналогии можно рассчитать остальные возможные варианты выигрыша и соответствующую вероятность.
|
X |
5 |
10 |
25 |
50 |
75 |
75 |
100 |
100 |
125 |
125 |
250 |
250 |
500 |
1000 |
|
p |
0,09 |
0,09 |
0,009 |
0,009 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
Таким образом, можно вычислить математическое ожидание участия:
.
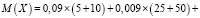
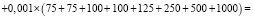
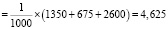Подводя итог сказанному, следует отметить, что однократная игра может быть несколько обоснованной, однако длительные попытки получить выгоду с подобной азартной игры не увенчаются успехом. Азартные игры являются лишь способом траты своего времени и денежных средств. С помощью математического обоснования удалось доказать невыгодность данного досуга. Что касается результатов исследования, то можно заключить, математическое ожидание может дать оценку наиболее выигрышной и удачной комбинации для игрока [3, 7].