Теория вероятностей – один из разделов математики, изучающий закономерности, которые присущиразличным случайным событиям. Данный раздел достаточно широко используютпри решении различных экономических задач, а так же в физике, биологии и в других областях науки.
Говоря о направлениях, в которых используется теория вероятности, начать по праву нужно со статистической физики. В современном естествознании большинство явлений природы носят статистический характер, а некоторые законы можно сформулировать исключительно при помощи применения терминов теории вероятностей [2].
Статистическая физика является основой всей современной физики, а теория вероятностей – ее математическим аппаратом. В статистической физике рассматриваются задачи, описывающие явления, которые определяют поведение большого числа частиц. Первый случай экспериментального исследования взаимосвязи между беспорядочным движением отдельных частиц и закономерным движением их больших совокупностей произошёл, когда в 1827 году ботаник Р. Броун открыл явление, которое по его имени названо «броуновским движением». Он наблюдал под микроскопом за цветочной пыльцой в воде. После чего он обнаружил, что взвешенные в воде частицы находятся в непрерывном беспорядочном движении, которое никак не получается прекратить, тщательно устраняя какие-либо внешние воздействия. Вскоре было обнаружено, что это общее свойство любых мелких частиц, которые находятся в жидкости. С тех пор броуновское движение стало классическим примером случайного процесса [3].
В молекулярной физике при помощи теории вероятностей описывают тепловые явления, в электромагнетизме – диэлектрические, в оптике она позволила создать теорию теплового излучения, молекулярного рассеивания света.Ярким примером применения теории вероятностей в физике является доска Гальтона, представляющая собой прибор из наклонной доски, на которой в определённом порядке закреплены штифты. Если с определённого места доски заставить катиться шарики соответствующей величины, то от столкновения с каждым штифтом они будут отклоняться от пути беспорядочным образом и, в итоге, собираются в приёмник на нижнем краю доски. Положение, которое они принимают в этом приёмнике обусловлено законом распределения ошибок Гаусса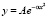 
. Также можно обозначить как n общее число столкновений шариков со штифтами, k – число раз, когда шарик поворачивает направо. Тогда число способов, которыми он может добраться до k столбика, определяется биноминальным коэффициентом 
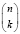. Отсюда следует, что вероятность оказаться в k-м столбике равна 
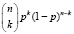, где p – вероятность поворота направо (обычно p = 0,5).
Интересным является то, что распределение шариков по секциям будет образовывать нормальный закон распределения. Доска не меняется, при этом шарики падают одни и те же, и, тем не менее, во-первых, форма распределения слегка колеблется (случайность), и разные шарики попадают в разные секции, во-вторых, на макроуровне, где проявляется организация шариков как совокупности, всегда получается нормальный закон распределения (закономерность). Такое распределение распространено в окружающем мире. Суммирование случайных величин, сумма действий, совместное наложение эффектов на микроуровне зачастую приводит, усреднившись, к появлению нормального распределения на макроуровне.
Понимание природы химических реакций, динамического равновесия также невозможно без статистических представлений. Вся физическая химия, ее математический аппарат и предлагаемые ею модели являются статистическими [5].
Биологи также заметили, что разброс размеров органов живых существ одного и того же вида укладывается в общие теоретико-вероятностные законы. Знаменитые законы Менделя, которые положили начало современной генетике, требуют вероятностно-статистических рассуждений. Изучение таких значительных проблем биологии, как передача возбуждения, устройство памяти, передача наследственных свойств, вопросы расселения животных на территории, взаимоотношения хищника и жертвы требует знания теории вероятностей и математической статистики. Многие задачи по генетике решаются именно на основе этих наук. Например, необходимо рассчитать, какова вероятность того, что следующий ребенок родится без аномалий, если в семье, где один из родителей имеет нормальное строение кисти (аа), а второй – шестипалый (Аа), родился ребенок с нормальным строением кисти. Как правило, ген полидактилии доминирует над геном, определяющим нормальное строение кисти. Посему введем обозначения: А-ген полидактилии, aa- «нормальный» ген.
Требуется провести анализирующее скрещивание. Для начала следует скрестить двух гомозиготных родителей: AA×aa, тогда, так как ген A – доминантный, вероятность рождения нормального ребенка 0 %, а как минимум 1 здоровый ребенок в семье есть. Если скрестить гетерозиготного родителя с родителем, гомозиготным по рецессивному признаку: Aa×aa у детей могут быть дети с генами: Аа Аа аа аа. В данном случае вероятность рождения нормального ребенка 50 %.
Наиболее широко в современных условиях теория вероятностей применяется при решении различных экономических задач. В качестве примера можнорассмотреть следующую задачу: пусть банк выдает кредит размером 3 млн. рублей на 1 год. Вероятность не погашения ссуды 10 %, соответственно вероятность погашения – 90 %. Доход кредитной организации является случайно величиной, так как заёмщик может как вернуть кредит, так и нет. Закон распределения этой случайной величины таков: p = 0,9; q = 0,1. Найдем математическое ожидание: 0,9р-0,1. Решив неравенство 0,9p-0,1 > 0, мы придем к тому, что, р > 0,1/0,9.Следовательно, ставка процента по кредиту должна быть выше 11 % [4].
Большое распространение теория вероятностей получила также в сфере страхования. В основе расчета нетто-ставок по страхованию жизнилежит вероятность наступления страхового случая [6]. При страховании на случай смерти страховым случаем является смерть в течение срока действия договора страхования. Вероятность дожить до определённого года зависит прежде всего от возраста страхуемого лица в момент страхования. На основании данных демографической статистики и теории вероятностей выявлена зависимость смертности от возраста людей, подчиняющаяся закону больших чисел. Вероятность дожития nPx лиц в возрасте х лет до возраста (x + n) лет определяется по формуле:
,
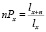где lx+n число доживающих до возраста x + n лет, lx число людей, доживающих до возраста x лет.
Вероятность смерти рассчитывается по формуле:
,
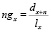где dx+n – число лиц, умирающих при переходе от возраста x лет к возрасту (x + n).
Рассмотрим пример, когда страховой компании необходимо найти вероятность страхового случая для мужчины 40 лет, используя данные таблицы смертности, а так же вероятность не наступления страхового случая в течение предстоящего года жизни. Известно, что 89102 человек дожили до возраста (x + n), а 89458 человек доживших до возраста x лет. Следовательно можно вычислить:
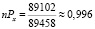
Что касается вероятности смерти, то:
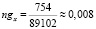
Исходя из этого, страховая фирма может предположить свои убытки в случае наступления страхового случая. В данной ситуации эта вероятность мала, ровно как и вероятность увеличения расходов фирмы.
Удивительно, но теория вероятностей применяется даже в гуманитарных науках. Статистические методы все в более значительной мере начинают привлекаться к историческим исследованиям, особенно в археологии. Статистический подход используется также для расшифровки надписей на языке древних народов. Расположение букв на клавиатуре компьютера определяется статистическим изучением частоты сочетаний букв в данном языке [1].
Исходя из всего сказанного, можно сделать вывод о том, что расчеты основанные на применении разделов теории вероятностей присутствуют в той или иной степени в различных сферах науки, в таких, как биология, физика, химия и современных экономических исследованиях. Большинство расчётов банковской и страховой сфер опираются именно на формулы теории вероятностей. Также немало важным является и то, что различные вероятностные теории присутствуют практически во всех сферах нашей повседневной жизни.