Математика и экономика – это самостоятельные отрасли знаний, каждая из которых обладает своим объектом и предметом исследования. Математика – наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов.
Экономика – хозяйственная деятельность общества, а также совокупность отношений, складывающихся в системе производства, распределения, обмена и потребления.
С древних времен и вплоть до XIX века математикой занимались лишь избранные. Развитию математики, а в частности именно в инженерных направлениях, способствовала промышленная революция, которая вызвала потребность в усовершенствовании и создании различных механизмов и различных разновидностей машин. Большой прорыв был сделан во второй половине прошлого века, когда достижения в области ядерной физики повлекли за собой дальнейшее развитие математики, математического образования и высокопроизводительных вычислений [3]. Подобные явления происходят и в наши дни, когда возникла необходимость управления многими социальными и различными экономическими процессами, которые являются предпосылкой к очередному витку в развитии математики. Экономика как наука в течение многих лет не вызывала внимание математиков, хотя есть единичные примеры математических работ XIX век, которые связанные с экономикой. В настоящее время в некоторых странах, а особенно в США, наблюдается процесс миграции многих ученых из классических для математики прикладных областей в экономику.
Широкое применение в экономических исследованиях занимают математические методы, основанные на математическом моделировании. Исследования строящиеся на статистической или вероятностной основе, позволяют учесть изменение факторов, которое практически полностью учесть не представляется возможным. Связи в экономической жизни, экономической динамики и поведение экономических субъектов прогнозирования основывается на построении теоритических моделей математическим методом -это важнейший инструмент анализа экономических явлений и процессов [8]. Для учёных всех стран мира математическое моделирование становится языком современной экономической теории. Например, задача о планирования работы предприятия – это пример использования математических моделей в экономике [5].
На сегодняшний день обширное использование математического аппарата в своих исследованиях способствует достижению наибольших успехов в данных областях. Поэтому применение математики на практике позволяет достичь более значительных результатов в изучении определенных явлений природы и общества [4].
Особенности математики, как отличительной области знаний, которые делают ее неповторимой, заключаются в следующем:
– не допущение никаких расхождений в определение правил и создания отношений – математических формул;
– математические формулы составляются из ряда аксиом, на основе строгих условий;
– возможность владеть теми или другими понятиями, не раскрывая их смысла [2].
Именно благодаря всем выше перечисленным особенностям математический аппарат и делается для всех отраслей знаний многофункциональным аналитическим инструментом.
Малоизвестные задачи, которые ставит экономика перед математикой, способствует ее стимулированию в поиске способов их решения. Потребности экономики на данный момент в новых математических методах превосходят способности математики [7]. Происхождение новых направлений в прикладной математике таких как: теории игр, программирования, массового обслуживания и некоторые другие – это экономическая действительность.
Развитию высокопрофессиональных знаний различных специалистов в отрасли экономики и управления способствует познание многих математических методов и это прежде всего характерный элемент развития. Именно кадровые работники являются пользователями различных аналитических инструментов, созданных математикой, следовательно, и обучать их математике нужно как пользователей, а не как математиков, объясняя им сущность математических терминов.
Для экономического анализа, статистических расчетов, организации различных внутрипроизводственных хозрасчетов и сокращения документа оборота предприятий и организаций все шире используют в экономической практике матричные методы, благодаря простоте их формул и богатому экономическому содержанию [6].
Матрицей называется таблица размером m×n прямоугольной формы состоящая из чисел и содержащая m количество строк и n количество столбцов и имеющая вид [1]:
A =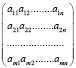 
.
Рассмотрим самое простое применение матрицы в различных отраслях экономики.
Возьмем предприятие, которое выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А. Вид сырья: 1, 2, 3, 4.
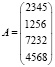
Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: при 60, 50, 35 и 40 ед.
Для начала составим вектор-план выпуска продукции
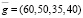
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; данный вектор затрат вычисляется как произведение вектора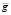 
на матрицу А:
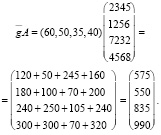
В этой задаче мы смогли с помощью матрицы составить ближайший план выпуска продуктов выполняемым предприятием по выпуску 4 продуктов из 4 видов сырья [9].
Экономико-математические методы это обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов.
Основным методом исследования систем является метод моделирования, т. е. способ теоретического анализа и практического действия, направленный на разработку и использование моделей. При этом под моделью понимают математическое описание исследуемого экономического процесса или объекта, которое выражает закономерности экономических процессов в абстрактном виде с помощью математических соотношений [2].
Рассмотрим задачу определения оптимального ассортимента продукции.
Предприятие изготавливает два вида продукции – П1 и П2 которые поступают в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. – для П1 и 4 д. е.
для П2.
|
Сырье |
Расход сырья на 1 ед. продукции |
Запас сырья, ед. |
|
|
П1 |
П2 |
||
|
A B |
2 3 |
3 2 |
9 13 |
|
Цена, д.е. |
3 |
4 |
|
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
Составим математическую модель задачи. Предположим, что предприятие изготовит х1 – единиц продукции П1 и х2 – единиц продукции П2.
Тогда система ограничений примет вид:
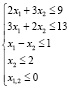
Доход от реализации продукции характеризуется целевой функцией, которая стремиться к максимуму: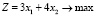 
.
В ходе решения получим оптимальный план задачи х1 = 2,4; х2 = 1,4. Подставляя значения х1 и х2 в линейную функцию, найдем: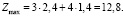 
Полученное решение означает, что объем производства продукции П1 должен быть равен 2,4 ед., а продукции П1 – 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д.е.
Таким образом, можно сделать существенный вывод, что две совершенно разные науки, такие как экономика и математика тесно взаимодействуют друг с другом. Узконаправленные математики или экономисты на сегодняшний день не нужны, а нужны подготовленные в двух различных направлениях специалисты. Все выше изложенное будет способствовать переходу к разработке разнообразных экономических программ с математической точностью и глубокими экономическими знаниями.