Одним из основных методов решения экономических задач является матричный метод. На данный момент особенно актуально использование матриц для создания баз данных, ведь вся информация обрабатывается и хранится в матричной форме.
Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов [4].
Впервые матрица появилась в Древнем Китае и носила название «волшебный квадрат». Чуть позже она стала известна и арабским математикам. В конце XVII века швейцарский ученый Габриэль Крамер разработал свою теорию, а в 1751 году опубликовал один из методов решения систем линейных уравнений «правило Крамера». Также в этот период был создан «метод Гаусса». Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы.
Таким образом, в математике появился раздел, который называется матричной алгеброй [6]. Матричная алгебра имеет очень важное значение в экономике. Обуславливается это тем, что матричный метод позволяет в достаточно простой и понятной форме записывать различные экономические процессы и объекты [1].
Матрица представляет собой упорядоченную систему информации, представленную в виде таблицы. Матрицей можно представить и систему информации о нормах материальных затрат для планирования снабжения предприятия [3]. Если предприятие производит n типов продукции, используя при этом m видов сырья, то матрица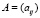 
размера 
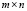определяет нормы материальных затрат. Так,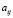 
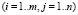– норма расхода i-го вида сырья на производство единицы j-го типа продукции [7].
Рассмотрим один из примеров использования матриц в экономике.
Пусть предприятие выпускает продукцию трёх видов P1, P2, P3 используя при этом три типа сырья S1, S2, S3. Нормы расхода сырья на единицу и расход сырья на один день представлены в таблице.
Требуется:
а) соcтавить экономико-математическую модель ежедневного выпуска продукции каждого из трёх видов P1, P2, P3, предполагая полное использование сырья;
б) найти ежедневный объём выпуска каждого вида изделий (систему решить матричным методом).
|
Тип сырья |
Расход сырья на 1 день, усл.ед. |
Нормы расхода сырья на единицу продукции, усл. ед. |
||
|
P1 |
P2 |
P3 |
||
|
S1 |
8900 |
7 |
4 |
2 |
|
S2 |
4550 |
2 |
3 |
2 |
|
S3 |
2350 |
0 |
1 |
5 |
Обозначим через x1, x2, x3 ежедневный объём выпуска изделий вида P1, P2, P3 соответственно.
Составим математическую модель задачи.
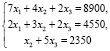(1)
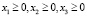(2)
Система линейный уравнений (1) с ограничениями (2) представляет собой экономико-математическую модель ежедневного выпуска продукции вида P1, P2, P3 [5].
Решив систему (1), найдем ежедневный объем выпуска продукции каждого вида в предположении полного использования сырья.
Перепишем систему (1) в матричном виде.
Матрица системы (1):
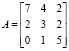
Матрица-столбец неизвестных:
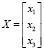
Матрица-столбец свободных членов:
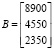
Тогда система (1) в матричном виде: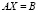 
.
Матрицу Х можно выразить, если умножить обе части этого уравнения слева на матрицу, обратную матрице А:
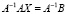
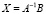
Это уравнение можно решить, если определитель матрицы А не равен нулю [2]:
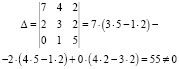
Обратная матрица будет иметь следующий вид:
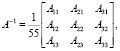
где Aij – алгебраические дополнения [8].
Транспонированная матрица имеет вид:
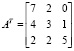
Найдем алгебраические дополнения.
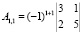
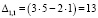
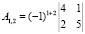
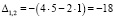
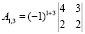
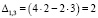
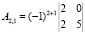
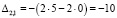
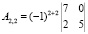
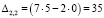
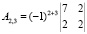
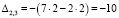
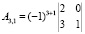
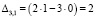
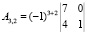
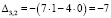
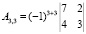
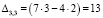
Обратная матрица равна:
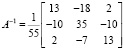
Так как,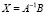 
значения неизвестных равны:
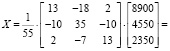
Таким образом, x1 = 700, x2 = 850, x3 = 300, т.е. ежедневный объем выпуска продукции вида P1 составляет 700 ед., продукции вида P2 составляет 850 ед., продукции вида P3 – 300 ед.
Из изложенного выше следует, что матрицы имеют ряд достоинств: позволяют в достаточно простой и понятной форме записывать различные экономические процессы и закономерности, дают возможность решать сложные задачи. Также с помощью матриц можно с минимальным количеством затрат труда и времени обработать большой статистический материал, различные данные, которые характеризуют структуру и особенности социально-экономического комплекса.