Обучение решению прикладных задач математическими методами не является задачей математических курсов, а задачей курсов по специальности.
Это положение касается одного из тех вопросов, по которому особенно часто критикуются как математические курсы в высших технических учебных заведениях, так и учебники по математике для них. Безусловно, что простейшие конкретные примеры, иллюстрирующие применение математических понятий для изучения реальных явлений, как-то: иллюстрация понятия производной скоростью движения материальной точки, интеграла – работой силы, составления дифференциальных уравнений – выводом уравнения радиоактивного распада и т.п. весьма полезны.
Однако, систематическое обучение применению математических методов, изучаемых ими в курсе математики, к решению прикладных задач обязательно должно осуществляться на профилирующих кафедрах. Это должно являться непреложной обязанностью этих кафедр. Только в этом случае у студентов может создаться убеждённость в полезности и необходимости знания и использования математических методов в его профессии.
Если на профилирующих кафедрах это не делается, то, возможно, это признак того, что для данной специальности вовсе и не нужна математика в том объёме, в котором она изучается в данном ВУЗе, а может быть, и признак неблагополучной постановки изучения в нём специальных дисциплин. Во всяком случае, существенно большая польза от изучения математики будет в том случае, когда в процессе всего обучения она будет достаточно широко использоваться при изложении специальных дисциплин, когда на старших курсах будут читаться нужные для специальности дополнительные главы математики, не входящие в основной курс, короче тогда, когда в ВУЗе будет осуществлено непрерывное математическое образование.
Смысл этого положения отнюдь не в разделе сфер влияния, а, наоборот, в эффективном сотрудничестве математических и специальных кафедр.
К математическим курсам нередко предъявляются претензии, что в них в недостаточном количестве выводятся дифференциальные уравнения, описывающие реальные явления. В этом вопросе следует чётко отдать себе отчёт в том, что математическое моделирование реальных явлений, т.е. составление математической модели такого явления, – это не задача математики.
Безусловно, что обучение умению составлять математические модели реальных явлений является одной из первоочередных задач в процессе образования специалистов, и потому этому должно уделяться гораздо больше времени и внимания, чем это часто делается.
Особенно следует подчеркнуть важность и необходимость для многих специальностей умения составлять не только детерминированные математические модели, но и вероятностно-игровые, умения выбирать и использовать для этого статистические и опытные данные, обрабатывая их в случае необходимости с помощью современной вычислительной техники.
Методика обучения математическому моделированию разработана в настоящее время совершенно недостаточно. Однако было бы неправильно возлагать основную работу в этом направлении на математиков. Главную роль здесь должны играть специалисты.
Не следует, конечно, думать, что математики не должны принимать участие в составлении математических моделей и обучать этому составлению. Совсем наоборот. Это не только желательно, но и необходимо. Хотя математическое моделирование не входит в математику, но оно входит в деятельность математиков. Поэтому обучение ему студентов должно проводиться совместно специалистами в соответствующих областях и математиками, но делаться это должно в специальных курсах на высоком профессиональном уровне.
Математическое моделирование заслуживает особенного внимания, поскольку оно играет все большую роль во многих областях современной науки и техники, являясь мощным и экономически выгодным средством для проведения научных исследований, так и для выполнения самых разнообразных экспериментальных и конструкторских работ. Например, использование математических моделей при проектировании технических систем и расчёт их на ЭВМ экономически во много раз более выгоднее создания экспериментальных образцов.
Однако математическое моделирование и проведение с помощью модели «математического эксперимента» дают не только экономическую выгоду, а существенно расширяют возможности эксперимента. Математический эксперимент можно провести для изучения явлений, которые в естественных условиях протекают столь медленно, что постановка реального эксперимента теряет всякий смысл. Более того, математический эксперимент можно применить для исследования таких ситуаций, которые мы просто не в силах воспроизвести в реальных условиях.
Не нужно, впрочем, думать, что математический эксперимент полностью заменяет реальный. Это не так, прежде всего потому, что математический эксперимент имеет дело не с самим явлением, а лишь с его математической моделью. Однако интересно и важно отметить, что математический эксперимент, как и всякий эксперимент, может привести к открытию новых реальных явлений, например, физических.
Таким образом, математическое моделирование в сочетании с современной вычислительной техникой даёт в руки учёных качественно новые методы исследования, качественно новые методы управления процессами как естественными, так и порождёнными деятельностью человека. Его широкое использование необходимо для успешного развития наук. Оно составляет неотъемлемую часть процесса накопления знаний человеческим обществом и приводит к необходимости подготовки специалистов нового типа, владеющих не только своей специальностью, но и математикой, знающих методы математического моделирования и умеющих их творчески использовать. Поэтому в наши дни должно быть затрачено особое усилие на подготовку специалистов, способных квалифицированно решать задачи математического моделирования.
Вопрос о подготовке таких специалистов делается сейчас одним из самых важных и актуальных вопросов современного образования. Правильная организация обучению составления математических моделей возможна лишь при хорошей координации усилий в этом направлении математиков и специалистов в соответствующих областях.
Рассмотрим пример построения математической модели при изучении темы «Системы линейных алгебраических уравнений».
Системы линейных алгебраических уравнений являются важным атрибутом при расчете сложных электрических цепей различными методами: по законам Кирхгофа, контурными токами, узловыми потенциалами. Остановимся на методе контурных токов [1].
Он основан на введение промежуточных неизвестных значений – контурные токи. Уравнения составляются по второму закону Кирхгофа. Метод удобно применять, когда число уравнений составленных по первому закону Кирхгофа, больше числа составленных по второму. [2]
Рассмотрим алгоритм расчета:
1. Вначале задаются токи ветвей;
2. Задаются направления контурных токов для каждого независимого контура;
3. При наличии идеальных источников тока, через него будет проходить контурный ток, равный величине источника
4. Для неизвестных контурных токов составляется линейное уравнение;
5. После определения значений контурных токов, определяются токи ветвей [3].
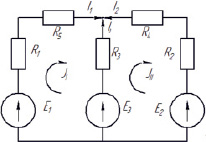
В качестве примера рассчитаем электрическую схему (рисунок).
Для схемы:
E1 = 15 B, E2 = 20 B, E3 = 17 B,
R1 = 12 Ом, R2 = 17 Ом, R2 = 25 Ом,
R2 = 17 Ом, R3 = 25 Ом,
R4 = 10 Ом, R5 = 15 Ом.
Два условия выполнены, пропуская пункт 3, переходим к 4.
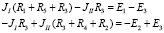
Методом Крамера решим эту систему, для этого составим квадратную матрицу R и матрицу-столбец Е:
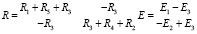
Находим определитель R:
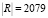
Находим значения J:
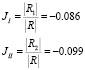
По первому закону Кирхгофа находим токи ветвей:
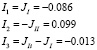
Для проверки составим баланс мощностей:
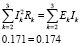
Небольшая разница обусловлена округления при расчетах.

