Переходным процессом называется процесс перехода из одного энергетического состояния электрической цепи к другому [1].
Расчет переходных процессов начинается с указания на схеме положительного направления токов и напряжений стрелками.
Порядок расчета переходных процессов классическим методом:
1. Единственный этап, в котором используется схема до коммутации. Рассчитаем эту схему в установившемся режиме и определим начальные условия [2].
2. Далее все этапы расчета используем схему после коммутации. Составим для t ≥ 0 характеристическое уравнение и определим корни.
3. Запишем уравнение для определяемого тока или напряжения в виде y(t) = yвын(t) + yсв(t). Для упрощения нахождения постоянных интегрирования расчет тока в индуктивности или напряжения на емкости рекомендуется вычислять для тех у кого известны независимые начальные условия. Вид составляющей yсв(t) можно определить по виду корней характеристического уравнения [3].
4. Для схемы после коммутации запишем систему дифференциальных уравнений для мгновенных значений токов и напряжений. Благодаря данной системе можно определить вынужденные составляющие токов и напряжений, а также зависимые начальные условия [4].
5. С помощью предыдущего пункта при t = ∞ определим yвын(t) известными методами расчета установившихся режимов.
6. Подставим в систему уравнений из пункта 4, записанную для t = 0+, найденные в пункте 1 независимые начальные условия, можем определить зависимые начальные условия.
7. Получив начальные условия, найдем постоянные интегрирования.
8. Запишем выражениее y(t) в окончательном виде и построим график полученной временной функции.
9. При помощи системы уравнений из пункта 4 можем найти остальные токи и напряжения.
Напряжение на индуктивности:
.
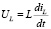Ток в емкости:
.
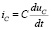Определим переходные процессы классическим методом:
Для схемы 1.1 определим закон изменения напряжения на емкости. Условия для решения: E = 120 B; R1 = R2 = R0 = 10 Ом; L = 0,1 Гн; C = 100 мкФ.
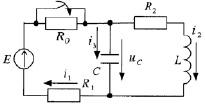
Схема
Из-за того что цепь подключена к источнику постоянного напряжения, то в установившемся режиме до коммутации емкость имеет бесконечно большое значение, а индуктивность имеет нулевое сопротивление
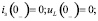
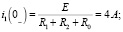
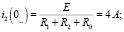
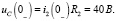
В соответствии с законами коммутации:
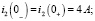
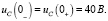
Корни характеристического уравнения будут равны:
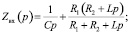
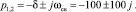
При комплексно-сопряженных корнях характеристического уравнения решение ищем в виде:
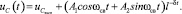
Далее используя уравнения для схемы после коммутации, определяем требуемое для нахождения постоянных интегрирования значение производной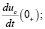 
[5]
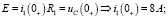
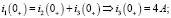
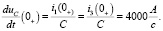
В установившемся режиме при t = ∞ вынужденная составляющая напряжения на емкости будет равна: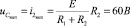 
[6].
Определяем постоянные интегрирования, используя найденные начальные условия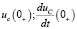 
. Для чего в систему уравнений:
;
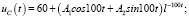
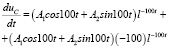для t = 0+ подставляем найденные значения:
;
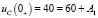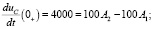
Отсюда:
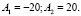
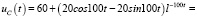
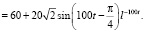
В настоящее время накоплен довольно богатый опыт использования вычислительной техники при решении дифференциальных уравнений и систем дифференциальных уравнений, накоплен и солидный пакет учебных и научных подпрограмм.
Компьютерный комплекс способен очень эффективно способствовать внедрению этих пакетов. Принцип состоит в том, что основное внимание уделяется именно практическим примерам применения таких пакетов.
Например, рассмотрев в электронном учебном пособии определенный раздел и разобрав несколько типовых примеров, можно прямо из текста пособия вызвать программу, которая реализует рассмотренный тип примеров в среде какого-либо интегрированного пакета.
Использование интегрированных пакетов стимулирует человека менять принцип подхода к решению задач. На первый план выходит комплексный подход к задаче – выработка принципа решения в общем, виде, т.е. главное – не только получение конкретного ответа на поставленный в задаче вопрос, но и нахождение общего алгоритма, что очень важно для современного специалиста-инженера.
Для того чтобы успешно использовать пакеты компьютерной математики, необходимо иметь представление об основных численных методах. Появление современных вычислительных систем значительно облегчает доступ к компьютеру непрофессионалов в области программирования, поддерживает интерес пользователя и стремление к освоению новых компьютерных технологий.
В нашем университете проводятся практические занятия с использованием компьютерной математической системы «Maple».
Данная система весьма популярна в научных кругах. Это очень надежный и устойчиво работающий Пакет, который кроме аналитических преобразований, в состоянии решать задачи численно. Особенностью данного Пакета является то, что ряд других программных продуктов используют интегрированный символический процессор Maple.
В качестве примера можно привести программу по теме «Решение системы линейных дифференциальных уравнений в компьютерной математической системе Maple».
Программа предназначена для отработки навыков решения системы линейных дифференциальных уравнений и представляет собой интерактивную электронную книгу, разделенную на секции и подсекции.
В секциях и подсекциях изложен порядок проведения практической работы, приведены примеры выполнения заданий.
В заключении, хочется отметить, что появление современных систем компьютерной математики позволяет качественно изменить подходы и методы изложения материала, сделать его наиболее доступным, наглядным, а значит и наиболее интересным и привлекательным, для основной массы студентов.