Первое упоминание о так называемых «мнимых» числах как о квадратных корнях из отрицательных чисел появилось ещё в XVI в. В 1545 г. итальянским учёным Д. Кардано (1501-1576) была проделана работа, в которой, пробуя решить уравнение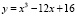 
, он получил 
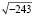. Через данное выражение представились действительные корни уравнения: 
, 
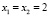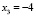. Заслуга Джироламо Кардано заключалась в предположении существования «несуществующего числа» 
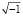, вследствие чего он ввёл правило умножения: 
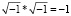[4].
Комплексные числа (КЧ) – это курс математики, наиболее удобный и подходящий для подготовки профессионального направления бакалавра по таким направлениям как: Информатика и вычислительная техника. Так же при изучение комплексных чисел важно учесть применение знаний математики в специальных, общетехнических дисциплинах, в частности в электротехнике [5]. Использование комплексных чисел даёт возможность применять формулы, законы и методы расчётов, применяющиеся в цепях переменного и постоянного токов, упростить некоторые вычисления, путём замены графического решения алгебраическим и рассчитать сложные электрические цепи, а так же упростить решения по расчётам цепей переменного и электрического токов [11, 13].
Для того, чтобы студент мог проводить математические операции с КЧ, он должен уметь: 1) находить модуль а аргумент комплексного числа и, наоборот, комплексное число по его аргументу и модулю; 2) переводить комплексное число из одной формы в другую; 3) производить умножение и деление, сложение и вычитание комплексных чисел [10].
Кроме этого, довольно важную роль занимает умение построения кривой и вектора по уравнению синусоиды, вектора по КЧ, определения КЧ по уравнению и вектору и уравнения по комплексному числу [6].
В теме «Переменный ток» занимает очень важное место в электротехнике, так как большая часть электротехнических установок работает на переменном токе, который в свою очередьизменяется по синусоидальному закону.
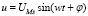
– уравнение переменного напряжения, где u – мгновенное значение напряжения; UM – макс. значение (амплитуда) напряжения; w – угловая частота; t – время; φ – начальный фазовый угол; wt = α – электрический угол. Данное уравнение объединяет (связывает) две переменные величины: напряжение u и время t. Напряжение изменяется синусоидально с течением времени [1].
Подобный вид имеют уравнения тока и Э.Д.С.:
;
.
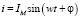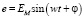Для того чтобы произвести расчёт цепей переменного тока используют синусоидально изменяющимися параметрами, т.е. выполнять сложение, вычитание, умножение и деление, приведённого выше типа уравнений .
Складывать синусоидальные величины довольно сложно, особенно при сложении большого числа уравнений [9, 12].
Переменная синусоидальная величина имеет следующие свойства:
1. Переменную синусоидальную величину можно представить определённо вектором. Длина этого вектора будет равна величине амплитуды, а угол наклона – начальномуфазовому углу соответственно.
2. Сложение и вычитание данных величин дозволено заменить сложением и вычитаем векторов.
Помимо сложения и вычитания синусоидальных величин требуется умножать и делить. Именно здесь нам помогают комплексные числа.
На плоскости комплексное число принято изображать в виде вектора, длина которого будет равна модулю данного числа, а угол наклона – его аргументу. В сравнении с математикой в электротехнике мнимое число принято обозначать буквой j. Если дано некоторое КЧ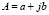 
, то его можно представить в виде вектора, где его модуль будет равен 
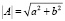, а его аргумент соответственно – 
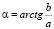[2, 14].
Комплексное число обладает тремя формами: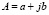 
– алгебраической; 
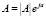– показательной; 
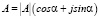– тригонометрической.
Комплексное число определённо представлено вектором, а определённому вектору соответствует определённое комплексное число [8].
Стало быть, что переменную синусоидальную величину мы можем представить комплексным числом, если:
а) переменную синусоидальную величину возможно представить вектором;
б) данному вектору соответствует конкретное комплексное число.
Комплексными числами можно выражать следующие величины: ток, напряжение, мощность, проводимость и сопротивление [3].
Напряжение и ток
Дано уравнение напряжения –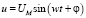 
. В электротехнике принято брать за длину вектора действующее значение, а не максимальное. Она находится (вычисляется) как частное максимального значения UM и 
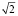, и обозначается буквой U без индекса:
;
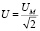Комплексом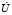 
– называется синусоидальная величина, которая выражена комплексным числом.
Комплекс напряжения, как и комплексное число можно записать в трёх формах:
а)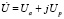 
– алгебраической;
б)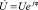 
– показательной;
в)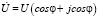 
– тригонометрической.
Следовательно, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, реактивная – мнимой части, активная составляющая – вещественной части комплекса напряжения [7, 15].
Аналогичные формы для тока:
;
;
;
;
.
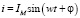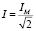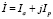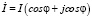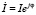Итак, комплексны числа (КЧ), как уже вначале говорилось, – это курс математики наиболее удобный для изучения такой дисциплины, как электротехника. Именно комплексные числа позволяют применять законы и формулы в цепях постоянного и переменного токов, упрощают различного вида вычисления и помогают рассчитывать сложные электрические цепи.