При изучении экономических явлений, процессов, обусловленных деятельностью человека, приходится рассматривать изменение одной величины в зависимости от изменения другой, описывая эти изменения функциональными зависимостями.
Многочисленные наблюдения и исследования показывают, что в окружающем нас мире величины (например, цена какого-либо товара и величина спроса на этот товар, прибыль фирмы и объем производства этой фирмы, инфляция и безработица и т. п.) не существуют изолированно друг от друга, а, напротив, связаны между собой определенным образом.
Современная экономическая наука характеризуется широким использованием математики. Математические методы стали составной частью методов любой экономической науки, включая экономическую теорию. Ее использование в единстве с обстоятельным экономическим анализом и новыми информационными технологиями открывает новые возможности для экономической науки и практики.
Рассмотрим зависимость суммарной величины у (затрат, дохода, прибыли и т. п.) от величины x, т.е. функция f(x), x>0 характеризующая объем производства, продаж, потребления и т. д. В большинстве случаев величина x не является целочисленной: либо она бесконечно делима и измеряется в тоннах, литрах, киловатт-часах и тому подобных единицах; либо измеряется в штуках, но настолько велика, что изменение на одну штуку совершенно неощутимо (например, часы или радиоприемники). Поэтому мы будем считать ее величиной непрерывной и ограничим лишь условием x>0,
Среднюю величину определим как частное
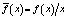. (1)
Изменение аргумента на величину Δx, т. е. переход от объема x к объему x+Δx, вызывает изменение суммарной величины от f(x) до f(x+Δx), Δf=f(x+Δx) – f(x).
Отношение Δf/Δx характеризует изменение суммарной величины на единицу приращения величины x. Но так как мы считаем величину x непрерывно изменяющейся, никакой «минимальной порции» приращения не существует, и предельная величина определяется как предел:
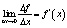, (2)
то есть представляет собой производную от суммарной величины по аргументу x (с чем и связаны термины «предельные затраты», «предельный доход» и аналогичные).
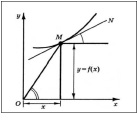
Рис. 1. Угол наклона к оси абсцисс кривой в точке M – это угол наклона касательной MN; он характеризует предельную величину fΔ(x). Угол наклона радиус-вектора OM характеризует среднюю величину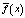 
Из графика видно, что с изменением объема x и средняя, и предельная величины изменяются, причем характер изменения этих величин различен. В дальнейшем среднюю величину f(x) и предельную – величину fΔ(x) будем рассматривать как функции объема x.
Когда суммарная величина пропорциональна аргументу, средняя величина f(x)=ax, совпадает с предельной при всех значениях х. Графиком такой зависимости служит прямая, проходящая через начало координат, а касательная к прямой – сама эта прямая, так что в рассматриваемом случае оба угловых коэффициента совпадают.
Рассмотрим теперь график суммарной величины, представленный на рис. 2,а. График зависимости затрат от объема производства как правило имеет вид выпуклой кривой и с ростом x наклон графика возрастает, так что fΔ(x) – возрастающая функция. Характер изменения средней величины иной. При возрастании x наклон радиус-вектора уменьшается от бесконечности до минимального значения, достигаемого в точке L, а затем вновь начинает возрастать.
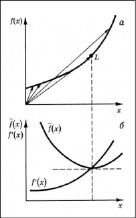
Рис. 2: а – кривая суммарной величины; б – кривая средней и предельной величин
Рассмотрим условия возрастания и убывания средней величины в общем случае. Равенство (1) позволяет представить суммарную величину в виде
.
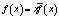Дифференцируя это выражение, получаем
,
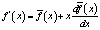откуда
.
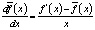Так как x>0, знак производной
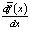
совпадает со знаком разности
.
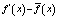Поэтому справедлива следующая теорема об изменении средней величины.
Если при данном значении x выполняется неравенство
,
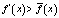то x – точка возрастания средней величины f(x); рис. 3,а,
Если при данном значении x выполняется неравенство
,
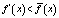то х – точка убывания средней величины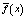 
, рис. 3,б.
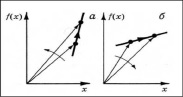
Рис. 3. Геометрическое представление условий: возрастания средней величины (а), убывания средней величины (б)
Из соотношения (3) следует также условие экстремума – максимума или минимума – средней величины. Если производная некоторой функции непрерывна, то сама эта функция достигает экстремальных значений в тех точках, где производная обращается в нуль. Таким образом, при непрерывном изменении предельной величины справедливо следующее условие локального экстремума средней величины: локальные максимумы и минимумы средних величин расположены в тех точках, в которых выполняется равенство
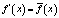. (4)