Любой хозяйствующий субъект в своей деятельности сталкивается с таким явлением, как риск. Он лежит в основе принятия всех управленческих решений.
Риск – это возможность возникновения неблагоприятной ситуации или неудачного исхода в производственно-хозяйственной или какой-либо другой деятельности.
Очевидно, что индивидуумы различаются своей готовностью пойти на риск. Некоторые не хотят рисковать, другим это нравится, а иные к риску безразличны (нейтральны).
Наиболее распространенное отношение к риску – это нерасположенность к нему.
Формальное объяснение феномена избегания риска предложил в XVIII веке швейцарский математик Даниил Бернулли. Бернулли обратил внимание на то, что многие люди, которые делают выбор в условиях неопределенности, не пытаются максимизировать ожидаемые денежные величины. Они скорее максимизируют ожидаемую полезность.
Бернулли предположил, что с ростом денежного дохода, его полезность возрастает, но с убывающей скоростью, т.е. мы можем говорить об убывающей предельной полезности дохода. Например, если доход какого-то лица 10000 долл. и он увеличивается на 1000 долл., то это увеличение дохода добавит к общей полезности больше, чем такой же прирост дохода – 1000 долл. при величине дохода 40000 долл. О человеке, функция полезности денежного дохода которого обнаруживает убывающую предельную полезность, говорят, что он не склонен к риску (risk averse).
Исследуем график функции полезности ЛПР, не склонного к риску, представленной на рисунке. Для такого типа ЛПР полезность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с вероятностью p выиграть М1 и с вероятностью (1 – р) выиграть М2.
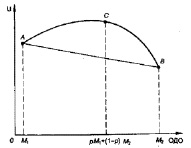
График функции полезности ЛПР, не склонного к риску
Формально мы имеем график вогнутой функции, о которой известно, что ордината любой точки кривой больше ординаты точки хорды кривой. Определим соотношение, характеризующее ЛПР, не склонного к риску. Нетрудно видеть, что
U(M1) – значение полезности в точке А;
U(M2) – значение полезности в точке В;
U(pM1 + (1 – р)М2) – значение полезности в точке С.
Уравнение хорды АВ имеет вид:
U1 = а + bМ,
где U1 – совокупность точек, лежащих на отрезке прямой.
Найдем значения параметров а и b уравнения прямой.
В точке А имеем U(M1) = а + bМ1.
В точке В имеем U(M2) = а + bМ2.
Вычитаем из первого выражения второе, исключая величину a:
U(M1) – U(M2) = b(M1 – М2),
откуда получаем:
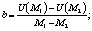
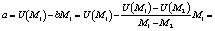
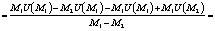
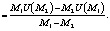
После подстановки значений для параметров а и b уравнение хорды АВ имеет вид:
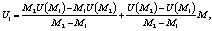
где М1 ≤ М ≤ M2.
Пусть М = рМ1 + (1 – р)М2,
где 0 ≤ р ≤ 1, тогда в точке С справедливо неравенство
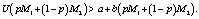
Подставив в это неравенство вычисленные значения а и b, получим:
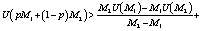
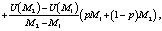
или
U(pM1 + (1 – р)М2) > PU(M1) + (1 – p)U(M2). (2)
Неравенство (2) характерно для функции полезности ЛПР, не склонных к риску. Оно действительно показывает, что полезность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с вероятностью р выиграть М1 и с вероятностью (1 – р) выиграть М2.
Аналогично можно показать, что для функций полезности ЛПР, склонных к риску, справедливо неравенство
U(pM1 + (1 – р)М2) < pU(M1) + (1 – p)U(M2). (3)
Для функций полезности ЛПР, безразличных (нейтральных) к риску, имеет место равенство:
U(pM1 + (1 – р)М2) = pU(M1) + (1 – p)U(M2). (4)
Склонность или несклонность ЛПР к риску, как уже отмечалось, зависит от его финансового положения, текущей ситуации принятия решения и других факторов. Иначе говоря, эта характеристика ЛПР не является абсолютной, присущей ему при любых обстоятельствах.

