Целью нашей работы стало применение Фурье-анализа для описания циклов колебаний проданных противовирусных препаратов и прогнозирование динамики будущих продаж на ближайший период.
Гармоническая модель продаж противовирусных препаратов позволяет отследить периоды заболеваемости и в зависимости от этого оценить необходимый объем закупок и будущую прибыль, а также выявить периоды, когда необходимо усилить меры по борьбе с вирусными заболеваниям.
Для изучения данной темы были проанализированы продажи компании-дистрибьютора лекарственных препаратов ООО ЦВ «Протек» г. Москва противовирусных препаратов за период с 2008 по 2014 г. в Москве и Московской области. По исходным данным построен график временного ряда (84 отсчета) по месяцам. (Рис 1).
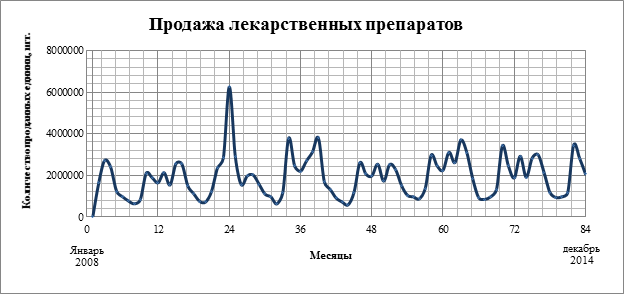
Рис. 1. Исходные данные
Так как данные реальные и не лишены субъективности, то существуют аномальные значения ряда. Они не отвечают потенциалу изучаемой системы, а их использование может сильно исказить получаемые (прогнозируемые) значения. Причинами аномальных наблюдений могут быть технические ошибки или ошибки первого рода: ошибки при агрегировании и дезагрегировании показателей, при передаче информации и другие технические причины.
Ошибки первого рода подлежат выявлению и устранению. Кроме того, аномальные уровни во временных рядах могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически, очень редко — ошибки второго рода; они устранению не подлежат. Однако, их можно заменить на усредненное значение.
Именно ошибки второго рода проявились в нашем примере. Для выявления конкретных значений аномального признака существует критерий Ирвина, который рассчитывается по формуле:
где 
- критерий Ирвина, 
- среднеквадратичное отклонение, которое рассчитывается по формуле:
Значения критерия Ирвина для разного количества результатов представлены в таблице ниже.
Таблица 1. Критерий Ирвина для n значений
|
n |
10 |
20 |
30 |
50 |
100 |
|
λ |
1,5 |
1,3 |
1,2 |
1,1 |
1,0 |
Согласно критерию, точка считается аномальной, если λi > λтаб. Табличное значение n = 84 заключено между 1 и 1,1.
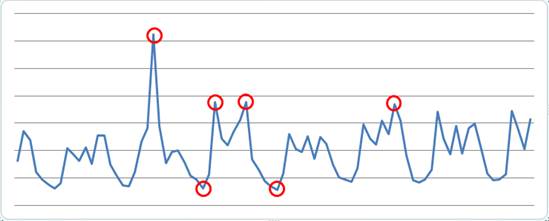
Рис. 2. Критерий Ирвина
Предварительная обработка заключается в выборе метода корректировки временного ряда так, чтобы прослеживающаяся тенденция не искажалась случайными отклонениями. В нашей работе мы произвели сглаживание методом взвешенной скользящей средней по 5 точкам
Тогда 
Однако не всегда методы механического сглаживания устраняют все неточности и аномалии реальных данных. Барьером к получению данных, пригодных для исследования, может служить тренд, т. е. общее направление развития процесса, определяющее основную тенденцию динамического ряда. Чтобы исключить воздействие на график случайных колебаний необходимо удалить тренд.
Для этого с помощью встроенной функции MSExcel с аналогичным названием строим линию тренда для наших данных. Двойной щелчок по линии тренда и выбор соответствующего свойства дает возможность отобразить ее уравнение.
Уравнение тренда в рассмотренном примере имеет вид: y = 5184,8x + 1600000.
Удалив тренд, получаем график, "очищенный" от случайных воздействий, который проходит немного ниже исходного. После проведения анализа Фурье для получения достоверного графика необходимо прибавить тренд к гармонической модели, описывающей исходную функцию.
Сам анализ Фурье заключается в том, что любую сложную форму волны можно представить в виде конечной и бесконечной суммы простых волн.
Полное гармоническое колебание описывается периодическими функциями sin kt и cos kt. Сложное гармоническое колебание возникает в результате суммирования при наложении простых гармоник друг на друга.
Для исследования исходных данных мы использовали следующее уравнение:
,
которое позволяет выравнивать процессы с периодичной составляющей k (определяет гармонику ряда).
Коэффициенты, необходимые для метода Фурье находят по формулам:
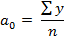
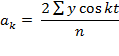
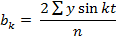
Отметим, что результаты по ряду Фурье дают наибольший эффект в тех случаях, когда временной ряд насчитывает большое число уровней.
В нашем случае коэффициенты получились следующие:
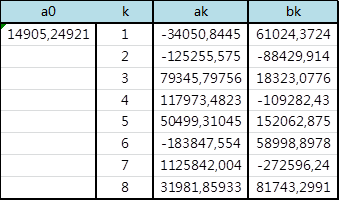
Рис. 3. Коэффициенты для анализа Фурье
Значения синусов и косинусов для дальнейших расчетов представляют в виде таблицы со следующими параметрами:
Таблица 2. Таблица для расчетов
|
Период времени |
t |
y |
y cos t |
y sin t |
y cos2t |
y sin t |
... |
Для изучения процессов с использованием ряда Фурье необходимо рассчитать несколько гармоник (чаще всего четыре), а затем установить, какая из них лучше отражает периодичность изменений. Формулы для гармоник выглядят так:
Так например, формула суммы восьми гармоник имеет вид:
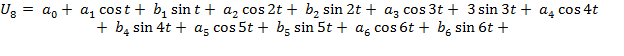
Для наших данных четырех гармоник оказалось недостаточно. По рис.5 видно, что сумма четырех гармоник не повторяет цикличность исходного графика:
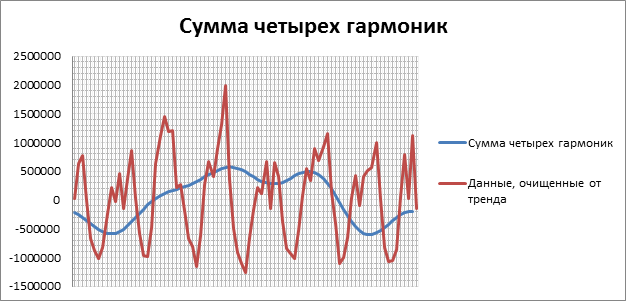
Формула суммы восьми гармоник с конкретными коэффициентами выглядит так:
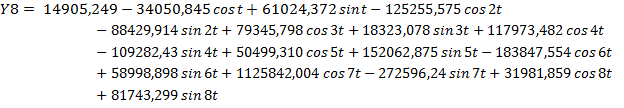
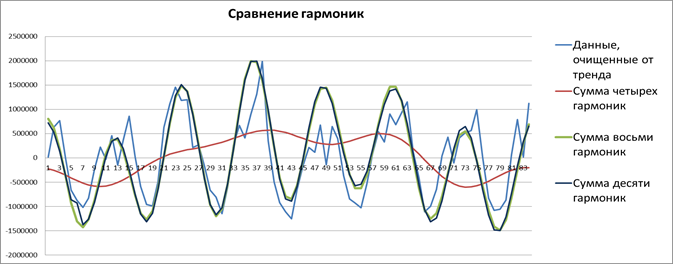
Изучая данные дальше и, строя десятую и двенадцатую гармоники, получается, что они практически совпадают друг с другом и восьмой гармоникой
Используя методы предварительной обработки данных и анализ Фурье, мы получили математическую гармоническую модель, описывающую исходные данные, на основе которой мы можем делать дальнейший анализ, включая прогнозирование.
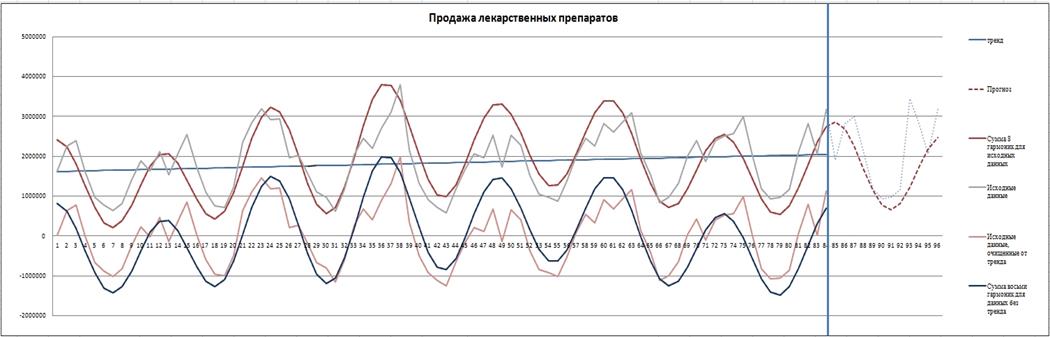
Рис. 5. Итоги
При проведении анализа Фурье неизбежны неточности. Поэтому необходимо посчитать погрешности- средняя ошибка аппроксимации. Формула погрешностей:
, где 
Выводы:
· Продажа лекарственных препаратов имеет цикличный характер, увеличивается и уменьшается в определенные временные периоды. (Увеличивается в осенне-зимний, уменьшается- в летний)
· Анализ данных позволяет сделать вывод о том, что пик продаж противовирусных препаратов приходится на декабрь- январь, а спад- на июнь- июль. Это обусловлено природой вирусных болезней. Иммунитет обессилен, нехватка витаминов и природные условия полностью способствуют этому.
· Прогноз продаж на следующий год приближен к реальности. Безусловно, на точность прогноза конкретной фирмы влияют множество факторов, например, такие, как: экономическая обстановка, рекламные акции других компаний и другие.
· Данный способ обработки имеет важное практическое значение, так как с помощью теоретических сведений, полученных в результате изучения, можно решать довольно широкий круг практических задач (менеджеры, экономисты и другие профессионалы, чье работа связана с обработкой данных). Можно исследовать многие социально- экономические явления.
· Средняя ошибка аппроксимации, т е. среднее отклонение расчетных значений от фактических составляет менее 2 процентов
· Несмотря на то, что расчетное значение коэффициента детерминации 
равно, 43%, он значим по критерию Фишера, а значит, модель значима в целом. Так как применяемый способ анализа изучает зависимость данных только от одного фактора- фактора времени, то существует другие регрессоры, оказывающие влияние на количество проданных противовирусных медикаментов, а значит, и на выручку от продаж.