Модели массового обслуживания часто встречаются в нашей повседневной жизни. Мы сталкиваемся с ними буквально повсюду: очереди в ожидании обслуживания в кафе, очереди к кассе в магазине, в банке, парикмахерской, автомойке, на бензозаправочной станции и т. д.
Анализ процессов массового обслуживания даёт нам оценку влияния на режим функционирования системы таких показателей, как частота поступления заявок на обслуживание, время обслуживания поступающих заявок, количество и размещение различных компонентов обслуживающего комплекса и т.д.
Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид
,
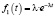где λ – интенсивность поступления заявок в систему (среднее число заявок, поступающих в систему за единицу времени).
Плотность распределения длительностей обслуживания:
,
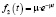где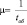 
– интенсивность обслуживания; tоб – среднее время обслуживания одного клиента.
Рассмотрим систему, работающую с отказами. Можно определить абсолютную и относительную пропускную способность системы.
Относительная пропускная способность равна доли обслуженных заявок относительно всех поступающих и вычисляется по формуле:
.
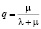Эта величина равна вероятности Р0 того, что канал обслуживания свободен.
Абсолютная пропускная способность – среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:
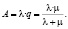
Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал обслуживания занят»:
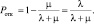
Величина Ротк может быть интерпретирована как средняя доля необслуженных заявок среди всех поданных.
Пусть одноканальная система массового обслуживания (СМО) с отказами представляет собой одно место в очереди к кассе в банке. Заявка – посетитель, прибывший в момент, когда место занято, получает отказ в обслуживании. Интенсивность потока прихода посетителей λ = 3 (чел./ч). Средняя продолжительность обслуживания tоб = 0,6 ч.
Мы будем определять в установившемся режиме следующие предельные значения: относительную пропускную способность q; абсолютную пропускную способность А; вероятность отказа Ротк.
Сравним фактическую пропускную способность системы массового обслуживания с номинальной пропускной способностью, которая была бы, если бы каждый посетитель обслуживался 0,6 часа, и очередь была бы непрерывной.
Вначале определим интенсивность потока обслуживания:
.
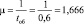Вычислим относительную пропускную способность:
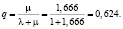
Величина q означает, что в установившемся режиме система будет обслуживать примерно 62,4 % прибывающих человек.
Абсолютную пропускную способность определим по формуле:
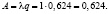
Это означает, что система способна осуществить в среднем 0,624 обслуживания человек в час.
Вычислим вероятность отказа:
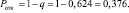
Это означает, что около 37,6 % прибывших посетителей на кассу получат отказ в обслуживании.
Определим номинальную пропускную способность системы:
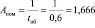(чел./ч)
Исходя из данных расчётов, делаем вывод, что Аном в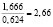 
раза больше, чем фактическая пропускная способность, вычисленная с учётом случайного характера потока заявок и времени обслуживания.
Данная система работает неэффективно. Вероятность отказа слишком большая – 37 человек из 100 уйдут из банка не получив обслуживания. Это недопустимо. В такой ситуации есть несколько решений проблемы:
Добавить ещё один канал обслуживания, т.е. организовать двухканальную систему. Это позволит принять больше заявок, но несёт дополнительные затраты на создание дополнительного канала и на дальнейшее его содержание.
Не добавляя ещё одного канала, уменьшить время на обслуживание одной заявки, например, за счёт автоматизации канала.
Не добавляя ещё одного канала, создать систему без отказов, но с ожиданием в очереди. Этого можно добиться, если установить диваны для ожидания.
Таким образом, можно повысить эффективность работы наиболее приемлемым для банка решением.